2021-01-15

Nets define Topologies

The standard definition of a topological space is in terms of open sets. We fix a collection $\mathcal{T}$ of sets that are open by definition, and have a few laws about the structure of this collection.

One motivation for Topology is the study of sequences generalized as much as possible. You can define sequences very generally as functions: $\mathbb{N} \to X$ for a space $X$, and study their convergence in this general setting.

One problem with sequences is that they're not sufficient to completely characterize topological spaces. For example, take the two following theorems:

If a space $X$ is Hausdorff, then every sequence converges to at most one point.

If there is a sequence inside a subset $S$ converging to $s$, then $s$ is a limit point of $S$.

We'd like to see if these statements hold in the other direction, but unfortunately, sequences are too constraining here, and we cannot prove the converse of these statements generally. We need to make assumptions about the structure of the space if we want to prove these things

Nets

Nets generalize sequences, and allow us to more fully characterize topological spaces. A sequence is just a function $\mathbb{N} \to X$, giving us a linear sequence of points in the space:

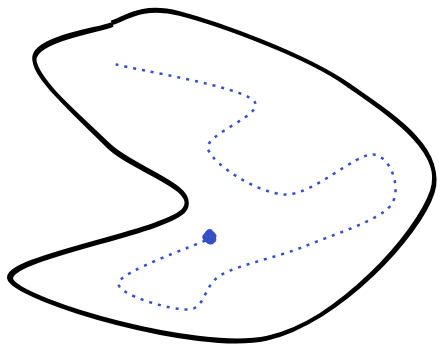
Nets generalize this by allowing threads of points that can temporarily diverge, so long as we have some kind of forward direction:

Formally, a Net is a function $J \to X$, where $J$ is a Directed Set.

A directed set is a partially ordered set $(J, \to)$ with the following extra property:

For any points $a, b \in J$, there exists $c \in J$, with $a \to c$ and $b \to c$. We call this being forward directed.

A partial order $\to$ on a set is a relation satisfying:

• $\forall a. \quad a \to a \quad$ (Reflexivity)

• $\forall a\ b\ c. \quad a \to b,\ b \to c \implies a \to c \quad$ (Transitivity)

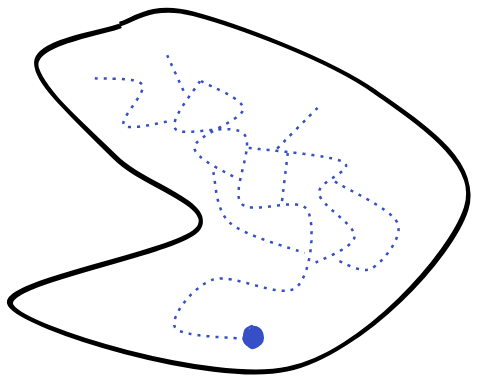
The crucial property of being forward directed means that we can't have multiple "tails" diverging off:

instead, these tails always meet back eventually. This is because we can take any two points on these different tails, and there will be some point that succeeds both of them.

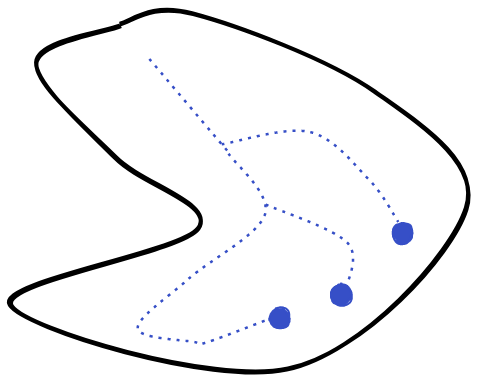
Formally, given a Net $f : J \to X$, a tail is a set of the form:

$f(a_\to) := \{f(b) \ |\ b \in J,\ a \to b \}$

This consists of all points in the net that come after a given position.

Examples of Directed Sets

It's clear that $\mathbb{N}$ is a directed set, under $\leq$, so sequences are also Nets.

Another good example of a directed set consists of a collection $\mathcal{C}$ of sets that is closed under pairwise intersection. We have $A \to B$ precisely when $A \supseteq B$. This is forward directed, since given $A$ and $B$, we can take $A \cap B$ as their common successor. Because the set $\mathcal{C}$ is closed under pairwise intersection, this is also an element of the collection.

We can generalize this to collections of sets where for any $A, B \in \mathcal{C}$, there exists $D \in \mathcal{C}$ with:

An example of such a collection would be a basis for a given topology.

Convergence

With this in hand, we can define convergence of a net.

A net $f : J \to X$ converges to a point $x \in X$ precisely when every neighborhood of $x$ contains a tail of $f$.

More concretely, this says that for every open set $N_x$ with $x \in N_x$, there exists a position $a$, such that for all $a \to b$, $f(b) \in N_x$.

Hausdorff

We can now complete the statement we made earlier about Hausdorff sets.

A space $X$ is Hausdorff precisely when every Net converges to at most one point.

Proof:

$\implies$

(This direction can be done with sequences)

Assume $X$ is Hausdorff. We show that if $f : J \to X$ is a Net converging to $x$, then if $f \xrightarrow{} y$, we must have $x = y$.

Assume $x \neq y$, but $f \xrightarrow{} y$. Because $X$ is Hausdorff, we have disjoint neighborhoods $N_x$ and $N_y$. Since $f$ converges to both $x$ and $y$, we have a tail $f(a_\to)$ and $f(b_\to)$ in each of these neighborhoods, respectively. The points $f(a)$ and $f(b)$ are in the respective tails, and must have a common successor, $f(c)$, by definition of a Net. This point is in both tails, and must therefore be in both $N_x$ as well as $N_y$. This contradicts the fact that $N_x \cap N_y = \emptyset$.

Therefore, $x = y$.

$\neg \implies \neg$

(This direction cannot be done with sequences)

Since $X$ is not Hausdorff, we have points $x, y$ such that every neighborhood $y \in U$ also contains $x$. We need to construct a Net converging to both.

Consider the directed set of neighborhoods of $x$, $\mathcal{N}(x)$. This is directed by virtue of being closed under finite intersection. We have $U \to V$ precisely when $U \supseteq V$.

Now, create a function $f : \mathcal{N}(x) \to X$ by picking a point $f(U) \in U$ for each neighborhood. Each neighborhood is nonempty since it must at least contain $x$ itself, so this is well defined, assuming choice.

It's clear that this converges to $x$, since any neighborhood $U$ of $x$ contains the tail $f(U_\supseteq)$.

Now, any neighborhood of $V$ of $y$ is also a neighborhood of $x$, so it also contains a tail.

Therefore, $f$ converges to $y$ as well.

$\square$

Note that this doesn't work out for sequences, because we don't have a freedom to construct a net that conforms so well to the structure of our topological space. If we can make assumptions, such as the neighborhoods around the point having some kind of countable structure, then we can recover this property.

Nets allow us to work in this general setting though.

Limit Points

As a reminder, a limit point of a set $S$ is a point $x$ such that every neighborhood of $x$ intersects $S$.

Nets allow us to more precisely capture the nature of limit points better than sequences.

A point $x$ is a limit point of $S$ precisely when there exists a net in $S$ converging to $x$.

$\impliedby$

(This direction works fine with sequences)

Every neighborhood of $x$ contains a tail in $S$ (by convergence), and thus a point in $S$.

$\implies$

(This direction doesn't work, since we can't always summon a sequence with the desired properties)

Take the directed set of neighborhoods $\mathcal{N}(x)$. Because each neighborhood of $x$ intersects with $S$, we can define a Net $f : \mathcal{N}(x) \to S$. This Net obviously converges to $x$, and is contained within $S$.

$\square$

Compactness

In a metric space, compactness is equivalent to every sequence having a convergent subsequence.

We can generalize this beyond metric spaces using Nets, but we first need to define sub-Nets.

Sub Nets

With sequences, the idea is that we take an increasing subset of the indices that never ends, and use that as our subsequence. With Nets, we need to take a directed subset, and also make sure that it never ends.

Given directed sets $J$ and $I$, a cofinal map is a function $g : I \to J$, such that:

• $a \to b \implies g(a) \to g(b)$
• For every $\alpha \in J$, there exists $a \in I$ such that $\alpha \to g(a)$

The first property just says that the inclusion from $I$ to $J$ can't completely obliterate all the properties of a directed set, which would give us subnets with a completely different structure.

The second property prevents us from "cheating" by taking an infinite net, and taking just a finite subnet. There always elements in the subnet succeeding us.

Concretely, a subnet of $f : J \to X$ is the composition $gf : I \to X$ of $f$ with a cofinal map $g : I \to J$.

Accumulation Points

Before we get to compactness, we first need to develop the notion of an Accumulation Point.

Formally, an Accumulation Point of a net $f : J \to X$ is a point $x$ such that for every neighborhood $U \ni x$, and position $\beta \in J$, there exists an $\alpha$, with $\beta \to \alpha$, such that $f(\alpha) \in U$.

Theorem: a point $x$ is an accumulation point of $f$ precisely when there is a convergent subnet $gf \xrightarrow{} x$.

Proof:

$\impliedby$

if $gf \xrightarrow{} x$, then we have, by definition of convergence:

Now, given some $U$, and some $\gamma \in J$, we need to find $\alpha \leftarrow \gamma$ with $f(\gamma) \in U$.

Consider this diagram:

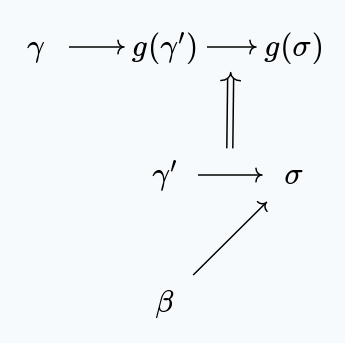
By the property of a subnet, we have some $\gamma'$ with $g(\gamma') \leftarrow \gamma$. Then, we can use the forward directeness to get a $\sigma$. Since $g$ preserves the partial order, we have $g(\gamma') \to g(\sigma)$. Finally, since $\sigma$ follows $\beta$, we must have $f(g(\sigma)) \in U$.

Thus, we pick $\alpha = g(\sigma)$

$\implies$

This other direction requires us to construct a convergent subnet, using the fact that $x$ is an accumulation point.

We first define a directed set:

We define:

That this is a partial order is straightforwardly proven. For forward direction, take $(\alpha, U)$ and $(\beta, V)$.

$W := U \cap V$ is also a neighborhood of $x$. There is a $\gamma$ with $\alpha \to \gamma$ and $\beta \to \gamma$. By definition of an accumulation point, we have a $\gamma' \leftarrow \gamma$ with $f(\gamma') \in W$.

Thus $(\gamma', W)$ is our forward.

From this directed set, we can define a cofinal map:

This obviously preserves ordering. As for cofinality, if we have $\beta \in J$, then $(\beta, X)$ projects down to $\beta$, and obviously $f(\beta) \in X$.

(this is in fact a bit stronger than cofinality)

We now show that this subnet converges to $x$.

Let $U$ be a neighborhood of $x$. Because $x$ is an accumulation point, $\exists \alpha$ such that $f(\alpha) \in U$. The position $(\alpha, U)$ is then the start of a tail of $gf$.

If $\alpha \to \beta,\ U \supseteq V$, then $f(\beta) \in V \subseteq U$, so this tail is indeed contained inside of $U$.

$\square$

Compactness and SubNets

Equipped with this key connection between accumulation points and convergent subsequences, we can prove that a subspace $C \subseteq X$ is compact precisely when every net in $C$ has a convergent subnet.

As a reminder, a subspsace $C$ is defined to be compact when every collection of open sets covering $C$ has a finite sub-collection covering $C$.

An equivalent characterization of compactness is:

A subspace $C$ is compact precisely when for every collection of closed sets with the finite intersection property, the intersection of the collection is non-empty.

A collection has finite intersection property iff finite intersections of its sets are non-empty.

Proof:

$\implies$

We assume that our space is compact, and we consider an arbitrary net $f : J \to C$.

Consider the set of tails:

This set has the finite intersection property. If we have: $f(\alpha_\to) \cap f(\beta_\to)$, then this is the set:

By forward directedness, ther always exists a $\gamma$ succeeding both $\alpha$ and $\beta$, so this set is non-empty.

By compactness, there exists a point $x$ in the intersection of all of these tails. This means that $\forall \alpha$ there exists a $\beta \leftarrow \alpha$, with $x = f(\beta)$.

But this means that $x$ is an accumulation point, for if $U \ni x$, and $\alpha \in J$, then $x = f(\beta) \in U$.

This is equivalent to there being a subnet of $f$ converging to $x$, as we've previously shown.

$\impliedby$

Consider an arbitrary collection of closed sets $\mathcal{A}$ with the finite intersection property. We want to show that $\bigcap_{A \in \mathcal{A}} A$ is non-empty.

Define $\mathcal{B}$ as the collection of finite intersections of sets in $\mathcal{A}$.

$\mathcal{B}$ is obviously closed under finite intersection, and so is a directed set under $\supseteq$, as we've shown earlier.

Now, by assumption, each element $B \in \mathcal{B}$ is non-empty, so we can define a subnet $f : \mathcal{B} \to C$ by picking a point $f(B)$ for each set.

To show that $\bigcap_{A \in \mathcal{A}} A$ is non-empty. We need to find $x$, such that $x \in A$, for an arbitrary $A$ in this collection.

Let $x$ be an accumulation point of $f$, which exists by assumption, and $A \in \mathcal{A}$. We now show $x \in A$.

Assume $x \notin A$, then $C - A$ is a neighborhood of $x$, since $A$ is closed. Now, since $x$ is an accumulation point of $f$, and $A \in \mathcal{B}$ there must be a $B \subseteq A$ with $f(B) \in C - A$. But, we also have $f(B) \in B \subseteq A$. This is a contradiction.

Therefore, we conclude that $x \in A$.

We've now shown that the intersection of an arbitrary collection of closed sets with the finite intersection property is non-empty, which shows that our space is compact.

$\square$

Equivalence with a Topology

So, we've seen that nets are sufficient to characterize quite a few topological properties. The cool thing about nets is that you can construct nets that mimic the structure inherent to any topological space.

In fact, knowing which nets converge is a complete characterization of a topological space.

A criterion is a mapping from nets $f$ and points $x \in X$ to truth values $\Omega(f, x) \in \{0, 1\}$, such that $\Omega(f, x) \implies \Omega(gf, x)$, for any subnet $gf$.

Evidently, a topological space induces a criterion, because convergence is defined for any topological space.

Induced Topology

More surprisingly, we can use a criterion to induce a topology on $X$.

First, note that we can equivalent define a topology in terms of its closed sets. We require that $\emptyset$ and $X$ are closed, the the finite union of closed sets is closed, and finally, that the arbitrary union of closed sets is closed. We can go from a closed topology to an open topology by taking the complements of sets.

A criterion $\Omega$ induces a closed topology on $X$, by defining a set $C$ to be closed precisely when for every net $f$ in $C$ we have

It's common knowledge that closed sets contain their limit points, and this characterization of closed sets inspires this definition.

We now show that this is a closed topology.

Now, since every $x$ is in $X$, then $X$ is obviously closed.

Now, $\Omega(f, x)$ is always false if $x \in \emptyset$, since it's impossible to even ask this question.

Intersections:

If you have some collection of closed sets $\mathcal{C}$, if $f$ is a net in $\bigcap \mathcal{C}$, then $f$ is also a net in any $C \in \mathcal{C}$. $\Omega(f, x)$ then implies $x \in C$, by assumption, and thus $x \in \bigcap \mathcal{C}$.

Union:

Let's say we take $A \cup B$, and $f$ a sequence converging to $x$. Define the restriction:

If $J|_A$ is not co-final in $J$, then there exists some $\beta$, such that for all $\alpha \leftarrow \beta$, $f(\alpha) \notin A$.

This would mean that the tail $f(\beta_\to)$ is contained in $B$, and that $J|_B$ is cofinal in $J$.

Without loss of generality, assume that $J|_B$ is cofinal. This provides us with a subnet of $f$ entirely contained in $B$, by only keeping the points of the net in $B$. This subnet converges to $x$ as well. By assumption, $B$ is closed, so $x \in B$.

Hence, $x \in A \cup B$.

$\square$

We could also define open sets directly, by saying that a set $U$ is open precisely when no net outside of $U$ can converge to a point inside of $U$. This is just a reformulation of what we've said so far.

Back and Forth

One remaining question is whether or not applying this construction twice gives you the same result.

Topology first

A topology $\mathcal{T}$ gives us a criterion $\Omega$ for convergence to a point. Does the induced topology $\mathcal{T}_{\Omega}$ equal $\mathcal{T}$?

Yes, simply because a closed set is completely characterized by the fact that it contains its limit points. We've shown that a limit point is just a point with a net converging to it. Our induced topology marks every set containing its limit points as closed, which matches are original topology exactly.

Criterion first

Now, if you have a criterion $\Omega$, then you have an induced criterion: $\Omega'$ by considering the usual convergence, but under the induced topology $\mathcal{T}_\Omega$.

It's pretty easy to show that $\Omega(f, x) \implies \Omega'(f, x)$, but I haven't yet been able to prove the converse.

It seems that in Kelley's General Topology, a few more axioms are required, and they might be able to patch this up.

Generalizations

The formulation of a topology in terms of a criterion invites generalizations. For example, you might relax the forward directedness and see what wacky spaces come out. You might also strengthen the conditions on the indexing set, and see what kind of strong properties of the space arise.