2021-04-21

Montgomery Ladder in ECC

This is a technique to efficiently calculate the x coordinate $\bold{x}(nP)$ given the x coordinate of a point on a Montgomery curve $\bold{x}(P)$ . This method is also easily implemented in a constant-time way.

This works for curves:

By^2 = x^3 + Ax^2 + x

Satisfying $B(A^2 - 4) \neq 0$ .

In Summary

The ladder itself

func ScalarMul(n Scalar, x Field) Field {
  nP := Projective{1, 0}
  n1P := Projective{x, 1}

  swap := 0
  for b := range n.msb .. n.lsb {
    swap ^= b
    condSwap(swap, nP, n1P)
    swap = b

    nP, n1P = step0(x, nP, n1P)
  }
  condSwap(swap, nP, n1P)
  return nP.X / nP.Z
}

Implementing the individual step:

// In field elements of course
const A24 = (A - 2) / 4

func step0(x Field, nP, n1P Projective) (Projective, Projective) {
  double_X := nP.X + nP.Z
  double_Z := nP.X - nP.Z
  // Addition
  add_X := n1P.X + n1P.Z
  add_Z := nP.X - nP.Z
  add_X *= double_Z
  add_Z *= double_X
  tmp := add_X - add_Z
  add_X += add_Z
  add_Z = tmp
  add_X.square()
  add_Z.square()
  add_Z *= x
  // Now we can do doubling
  double_X.square()
  double_Z.square()
  // Store for later
  Xn_plus_Zn_squared := double_X
  double_X *= double_Z
  tmp = Xn_plus_Zn_squared - double_Z
  double_Z = A24 * tmp
  double_Z += Xn_plus_Zn_squared
  double_Z *= tmp
  return (
    Projective{double_X, double_Z},
    Projective{add_X, add_Z}
  )
}

This could be optimized to reuse nP and n1P's buffers better as well

Doubling Formula

Given a point $P = (x, y)$ , the formula for $2P$ is given by:

\begin{aligned} &x_2 = B \lambda^2 - A - 2x \cr &y_2 = \lambda (x - x_2) - y \end{aligned}

where:

\lambda = \frac{3x^2 + 2Ax + 1}{2By}

(This formula is derived geometrically. $\lambda$ is the slope of the tangent line to the curve at the point $P$ .)

Because $\lambda^2$ features $By^2$ in the denominator, we can replace that with $x^3 + Ax^2 + x$ , and then calculate out the following identity:

x_2 = \frac{(x^2 - 1)^2}{4(x^3 + Ax^2 + x)}

This formula calculates $\bold{x}(2P)$ given only $\bold{x}(P)$ , and can be shown to be valid in other edge cases. See: ¹.

Projective Form

If we use projective coordinates, then we have $x = X / Z$ . Plugging this into the formula we had above, we get:

x_2 = \frac{(X^2 - Z^2)^2}{4ZX(X + AXZ + Z^2)}

In other terms, this means we have:

\begin{aligned} &X_2 = (X^2 - Z^2)^2 \cr &Z_2 = 4XZ(X + AXZ + Z^2) \end{aligned}

If we calculate this directly, a point doubling takes:

2 \bold{M} + 3 \bold{S} + 2 \bold{C}

We can re-arrange things to allow more sharing:

\begin{aligned} &X_2 = (X + Z)^2(X - Z)^2 \cr &Z_2 = ((X + Z)^2 - (X - Z)^2)\left( (X + Z)^2 + \frac{A - 2}{4}((X + Z)^2 - (X - Z)^2) \right) \end{aligned}

If you note that:

(X + Z)^2 - (X - Z)^2 = 4XZ

The correctness of this formula becomes relatively clear.

This adjusted formula takes:

2 \bold{M} + 2 \bold{S} + \bold{C}

Addition Formula

In can be shown that given $P$ and $Q$ , we have:

\bold{x}(P + Q)\bold{x}(Q - P) = \frac{ (\bold{x}(P)\bold{x}(Q) - 1)^2 }{ (\bold{x}(Q) - \bold{x}(P))^2 }

(This is a monstrous PITA, see ¹.)

In projective coordinates $[X_P, Z_P],\ [X_Q, Z_Q]$ , we get:

\bold{x}(P + Q) \frac{X_{Q - P}}{Z_{Q - P}} = \frac{(X_P X_Q - Z_P Z_Q)^2}{(X_Q Z_P - X_P Z_Q)^2}

This gives us the following formulas for addition:

\begin{aligned} &X_{P + Q} = Z_{Q - P}(X_P X_Q - Z_P Z_Q)^2 \cr &Z_{P + Q} = X_{Q - P}(X_Q Z_P - X_P Z_Q)^2 \end{aligned}

Unlike with doubling, we need to have calculated $P - Q$ prior. In practice, this constraint is easily accomodated.

This formula requires:

6 \bold{M} + 2 \bold{S}

To simplify it, first note that because of the properties of projective coordinates, multiplying both $X$ and $Z$ by $4$ gives us the same point:

\begin{aligned} &X_{P + Q} = 4Z_{Q - P}(X_P X_Q - Z_P Z_Q)^2 \cr &Z_{P + Q} = 4X_{Q - P}(X_Q Z_P - X_P Z_Q)^2 \end{aligned}

A bit of toil gives us the following formula:

\begin{aligned} &X_{P + Q} = Z_{Q - P}( (X_P - Z_P)(X_Q + Z_Q) + (X_P + Z_P)(X_Q - Z_Q) )^2 \cr &Z_{P + Q} = X_{Q - P}( (X_P - Z_P)(X_Q + Z_Q) - (X_P + Z_P)(X_Q - Z_Q) )^2 \cr \end{aligned}

This gives us an improved:

4 \bold{M} + 2 \bold{S}

In practice, we'll always have $Z_{Q - P}$ as $1$ , and $X_{Q - P}$ as a small constant, giving us:

2 \bold{M} + 2 \bold{S} + \bold{C}

Combined Formula

In practice, you have $(X_2, Z_2)$ and $(X_3, Z_3)$ , and calculate $(X_4, Z_4)$ as well as $(X_5, Z_5)$ together, giving you the following combined formula:

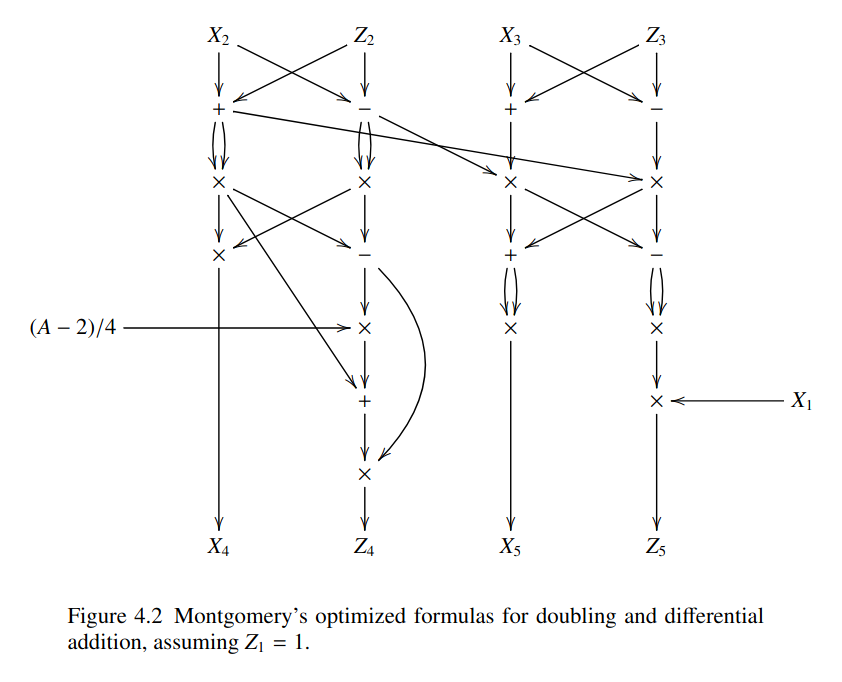
(See: ¹)

Ladder

One simple way to calculate $kP$ is as follows. Iterate over the bits of $k$ from most to least significant. If a bit $b = 0$ , set:

P \leftarrow 2P

If $b = 1$ , then set:

P \leftarrow 2P + P

Our addition formula works well when we have $P_n$ and $P_{n + 1}$ , and want to calculate $P_{2n + 1}$ , since the difference is $P_1 = P$ , a point we already know.

At each iteration, as we rise up to $P_k$ , our final value, we want to keep this property, and keep the successive values around.

This, when $b = 0$ , we do:

(P_n, P_{n + 1}) \mapsto (P_{2n}, P_{2n + 1})

The first value comes from point doubling $P_n$ , and the second from differential point addition, using the fact that the difference is $P_1$ .

When $b = 1$ , we want to do:

(P_n, P_{n + 1}) \mapsto (P_{2n + 1}, P_{2n + 2})

We can calculate the first value through point addition, and the second through point doubling.

In fact, if we define these two functions as $\text{step}_0$ , and $\text{step}_1$ respectively, we notice that $\text{step}_1$ comes from swapping the input, and then the output. With:

\text{swap}(P, Q) := (Q, P)

We have:

\text{step}_1 = \text{swap};\text{step}_0;\text{swap}

Thus, an algorithm for doing our ladder would be:

for b in bits:
  if b == 1:
    swap(P, Q)
  (P, Q) = step0(P, Q)
  if b == 1:
    swap(P, Q)
return P

We can make this "constant-time", by replacing our branching with a conditional swap:

for b in bits:
  cswap(b, P, Q)
  (P, Q) = step0(P, Q)
  cswap(b, P, Q)
return P

If we have two conditional swaps chained together

cswap(bits[i], P, Q)
cswap(bits[i - 1], P, Q)

Which happens between iterations, notice that this is effectively:

cswap(bits[i] ^ bits[i - 1], P, Q)

because of this, we can effectively do:

cswap(bits[N - 1], P, Q)
step0(P, Q)
cswap(bits[N - 1] ^ bits[N - 1], P, Q)
step0(P, Q)
...
cswap(bits[1] ^ bits[0], P, Q)
step0(P, Q)
cswap(bits[0], P, Q)

Noting that 0 ^ bits[N - 1] = bits[N - 1], we can effectively do:

swap := 0
for b in bits:
  swap ^= b
  cswap(swap, P, Q)
  swap = b
  step0(P, Q)
cswap(swap, P, Q)
return P

This allows us to efficiently compute whether or not we need to swap.

This is the gist of things, see the summary up top for more useable pseudo-code.

References

[1] Bernstein, Daniel J., Lange, Tanja - Montgomery Curves and the Montgomery Ladder (2017)