Discrete, Indiscrete: Free, CoFree

This note is about the discrete topology $X^{\bullet }$ and indiscrete topology $X_{\circ }$ on a set $X$.

Namely, ${-}^{\bullet }$ and ${-}_{\circ }$ are functors $\mathbf{Set}\to \mathbf{Top}$ with the following adjunctions with the forgetful functor $?:\mathbf{Top}:\mathbf{Set}$

$$\bullet ⊢?⊢\circ$$

As a reminder, the discrete topology contains all subsets of $X$

$${\mathcal{T}}^{\bullet }:=\{U|U\subseteq X\}$$

The indiscrete topology contains only the empty set, and all of $X$:

$${\mathcal{T}}_{\circ }:=\{\varnothing ,X\}$$

Note:

I like this notation, since the $\bullet$ denotes that the discrete topology is nice and full of sets. The $\circ$ denotes that the indiscrete topology is empty and devoid of any sets.

It’s clear that ${\mathcal{T}}_{\circ }$ is the coarsest topology on $X$, and ${\mathcal{T}}^{\bullet }$ is the finest topology on $X$. Formally, for any other topology $\mathcal{T}$ on $X$, we have:

$${\mathcal{T}}_{\circ }\subseteq \mathcal{T}\subseteq {\mathcal{T}}^{\bullet }$$

This is a very structural point of view, focusing on different topologies we can apply to $X$. We can shift our view to an external point of view, focusing on what continuous maps exist on the spaces $X^{\bullet }$ and $X_{\circ }$.

Discrete Topology

The discrete space $X^{\bullet }$ on a space $X$ can be characterized as follows. Any set function $X\to Y$ is continuous, provided $Y$ is a topological space.

Proof

Since every set of $X^{\bullet }$ is open, every pre-image $f^{-1}(V)$ of an open set $V$ is also open, so $f$ is open.

As a simple corollary, since we have $1:X\to X$, we can see that $X^{\bullet }$ is finer than all other topologies on the same set.

As a functor

Because of this property, we see that ${-}^{\bullet }:\mathbf{Set}\to \mathbf{Top}$ is a functor, sending a set $X$ to the discrete topological space $X^{\bullet }$. Set functions $f:X\to Y$, are already continuous functions $X^{\bullet }\to Y^{\bullet }$, because of the characterization we went over. The composition laws clearly hold, since functions are left untouched.

With this in mind, we have an even more powerful characterization:

For any set $X$, the space $X^{\bullet }$ is initial in the category $X\downarrow ?$, where $?$ is a forgetful functor $\mathbf{Top}\to \mathbf{Set}$.

More concretely, we have this situation:

Given any set function $f:X\to ?T$, where $T$ is a topological space, there exists a unique continuous map $\phi !:X^{\bullet }\to T$ such that the following commutes:

Proof

$X^{\bullet }$ satisfies this property. For each point $x\in X$, we need $f(x)=(\phi !\circ id)(x)=\phi !(x)$, so we have no choice but $f$. Since $X^{\bullet }$ is discrete, $f$ is necessarily continuous.

$\square$

Intuition

$X^{\bullet }$ is a way of creating a topological out of $X$ such that every set function out of $X$ becomes continuous.

Dual Property

Another property is that $?T$ is terminal in the slice category ${-}^{\bullet }\downarrow T$:

Given any set $A$ and continuous map $\varphi :A^{\bullet }\to T$, there exists a unique set function $f:A\to ?T$ such that this diagram commutes:

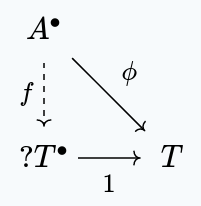
Proof

We need $f(a)=\varphi (a)$, so $f$ is uniquely determined as $\varphi$.

$\square$

With these two diagrams in place, we have an adjunction:

$$\bullet ⊢?$$

Indiscrete Topology

Any function $T\to X_{\circ }$ is continuous, since the only open sets are $\varnothing$ and $X$, whose preimages are $\varnothing$, and $T$ respectively.

$X_{\circ }$ is terminal in $?\downarrow X$.

If $T$ is a topological space with a set function $f:T\to X$, then there exists a unique continuous map $\phi !:T\to X_{\circ }$ such that the following diagram commutes:

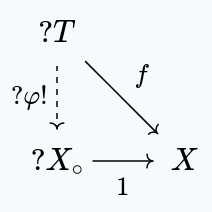
Proof

We have, once again, no choice but $\phi !=f$. This function is continuous, since any function to $X_{\circ }$ is continuous.

Intuition

This is really just a repetition of the fact that every set function $\to X$ becomes a continuous map $\to X_{\circ }$.

Dual Property

We have a similar dual property as before.

$?T$ is initial in $T\downarrow {-}_{\circ }$.

Given some set $A$ with a continuous map $\varphi :T\to A_{\circ }$, there exists a unique set function $f!:?T\to A$ making the following commute:

Proof

We necessarily have $f!(t)=\varphi (t)$.

These two properties form an adjunction:

$$?⊢\circ$$

Combining it all

Looking at both of these in unison, we have the following adjunction:

$$\bullet ⊢?⊢\circ$$

So, $\bullet$ is the typical left adjoint Free functor, and $\circ$ is a right adjoint Co-Free functor. So these two constructions are naturally dual to eachother.

$bullet$ allows us to make a topological space so that mapping out of the space is always continuous, and $\circ$ allows us to make a topological space so that mapping into the space is always continuous.

Furthermore, these defining properties are characteristic, so any space satisfying these properties must be homeomorphic.