Connectedness and Constant Maps

The usual definition of a connected space is something like:

A topological space $X$ is connected if it cannot be written as the disjoint union of open sets.

In more formal terms, if there do not exist $U,V$ open and nonempty, with $U\cap V=\varnothing$, and $U\cup V=X$, then $X$ is connected.

We call such $U,V$ a separation of $X$.

A slightly more useful definition is:

A topological space $X$ is connected if and only if every continuous map to $\{0,1\}$ (with the discrete topology) is constant.

One way of thinking about this, is that you can only assign different colors to parts of a space (in a continuous way) if that space is disconnected.

If a space is connected, then it only has a single color:

The equivalence of these two definitions is pretty easy to show:

If there exists a non constant map $f:X\to \{0,1\}$, then the preimages $f^{-1}(\{0\})$ and $f^{-1}(\{1\})$ provide us with a separation of $X$. (These serve as the “blue” parts, and the “red” parts, going with our previous analogy).

If there is a separation $U,V$ of $X$, then the map:

$$f(x)=\{\begin{array}{l}0x\in U\\ 1x\in V\end{array}$$

is continuous, and nonconstant.

Simpler Proofs

Many proofs become simpler under this paradigm. For example:

Let $\{A_{\alpha }\}$ be a collection of subspaces of $X$, each of which is connected. If ${\bigcap }_{\alpha }{A}_{\alpha }\ne \varnothing$, then ${\bigcup }_{\alpha }{A}_{\alpha }$ is connected.

Proof:

Let $f:{\bigcup }_{\alpha }{A}_{\alpha }\to \{0,1\}$. Let $p\in {\bigcup }_{\alpha }{A}_{\alpha }$ be a point in the intersection.

Because $A_{\alpha }$ is connected, $f$ is constant on $A_{\alpha }$, and equal to $f(p)$ everywhere. $f$ is thus constant on ${\bigcup }_{\alpha }{A}_{\alpha }$.

$\square$

Constant On Fibers

This way of looking at things is quite elegant if you adopt a more categorical point of view in other parts of Topology. For example, one characterization of a quotient map is as follows:

A continuous function $\pi :X\to Y$ is a quotient map if and only if for every function $f:X\to Z$ that is constant on the fibers ${\pi }^{-1}(\{y\})$ of $Y$, there exists a unique $g:Y\to Z$ making the following diagram commute:

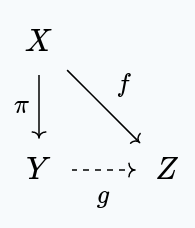
The following theorem becomes very simple with these definitions:

If $\pi :X\to Y$ is a quotient map, $Y$ is connected, and furthermore, every fiber ${\pi }^{-1}(\{y\})$ is also connected, then $X$ is connected.

Proof:

Take an arbitrary map $f:X\to \{0,1\}$. Because each fiber is connected, this map is constant on fibers. By the universal property of quotients, we have $f=g\circ \pi$, for some unique $g:Y\to \{0,1\}$. Since $Y$ is connected, $g$ is constant. This means that $f$ is constant, so $X$ is connected.

$\square$

(I first saw this proof, and other ideas, in “Topology: A Categorical Approach”)