A toy blockchain in Haskell, simulation-based security, and tinkering on Cryptographic foundations.

Omocha

The main programming project I’ve been working on is a “toy” blockchain, written in Haskell. I’m calling it omocha, which is Japanese for toy.

I say “toy”, in the sense that I’m not intending it to be used seriously. Rather, the purpose of the project is mainly to write a minimum viable example of a blockchain, implementing all the necessary components from scratch, albeit to a standard below production-level. The point is to spend more time learning novel aspects of how these systems work, rather than optimizing them using techniques I already know.

My goal here is to eventually have a simple Proof-of-Work blockchain, similar to Bitcoin. One thing I’m curious to learn about is the underlying structure of the Peer-to-Peer architecture underpinning everything. You hear a lot of talk about the Cryptography in Cryptocurrency, but less and less about the underlying P2P communication layer. For example, when you create a transaction, and broadcast it to miners, how do you actually go about doing this broadcast? How do nodes receive the data in a block when it gets mined? How do nodes handle reorganizations of the chain? These are the kinds of questions I hope to get answers to. Ultimately, I’ll have to figure out some solution to these questions, at least if I want to implement the project.

I’ve wanted to do a project in Haskell for a while, so this was a good occasion to pick it back up. I had initially planned on doing Rust, but then I started looking at how to interoperate between Rust and Haskell, and caught a bit of a brain parasite convincing me to try mixing the two to create this fun little project.

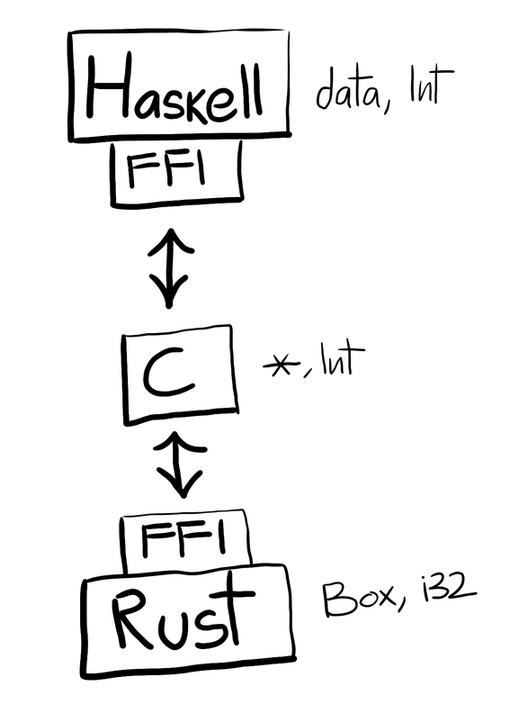
I’m still using Rust for the Cryptography though. For example, I use a Schnorr signature scheme over Ristretto, and I implemented that in Rust. To access it through Haskell, I went through Haskell’s FFI.

Haskell’s FFI has very few types, and is mainly designed around C. The only useful things we can pass around are int and *. Because of this, you have to contort the Rust API a little bit. And because you’re working in Rust, and not C, you also have to do a little massaging at that layer as well:

When you’d want to have a ByteString in Haskell, that becomes a function that takes a pointer, and writes to it:

foreign import ccall unsafe "signature_generate_private_key"
  c_signature_generate_private_key :: Ptr Word8 -> IO ()

There’s a convenient function create:

create :: Int -> (Ptr Word8 -> IO ()) -> IO ByteString

Which lets you then use this initialization function in order to create a ByteString on the Haskell side.

So, passing around bytes is somewhat easy.

What’s more difficult is passing around a more complicated structure.

The public keys for my scheme are a point on the Ristretto curve, which is a complicated Rust struct. Now, I could represent public keys as just the compressed bytes of this point, but I like the idea of parsing the bytes into a valid public key on the Haskell side, rather than having signatures potentially fail to verify because the public key is bad. This kind of API feels more Haskelly to me.

To pass this thing around, the simplest way I found was to use an opaque representation. Basically, on the Rust side, we have:

#[no_mangle]
pub extern "C" fn signature_private_key_to_public_key(
    private_ptr: *const u8,
) -> Box<signature::PublicKey> {
    Box::new(unsafe { signature::PrivateKey::from_pointer(private_ptr) }.public_key())
}

Which we can sort of think of as Rust using malloc to create space for this object, and then passing the pointer over to Haskell land. Our intention is to pass ownership of this object from the Rust side to the Haskell side:

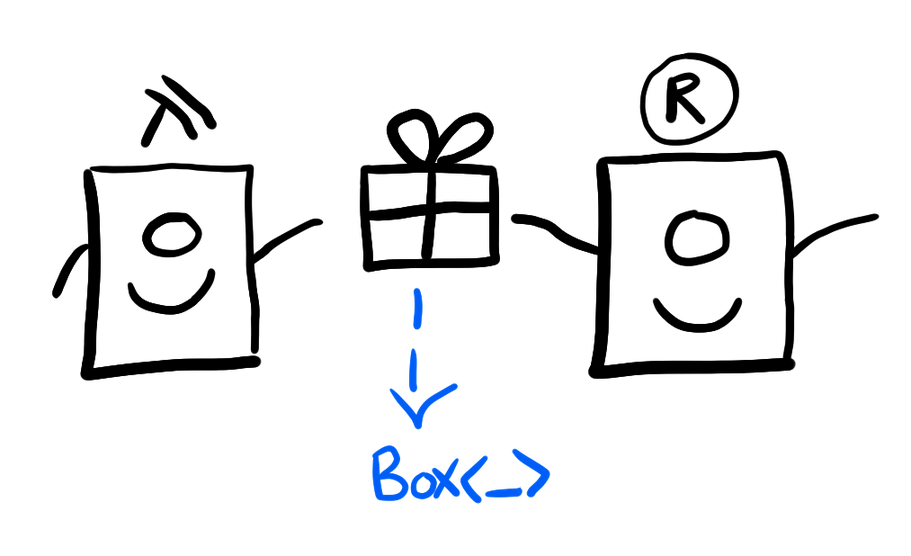
This also means that the Haskell side is responsible for freeing that memory itself. We do this by attaching a finalizer to that object, using the ForeignPtr type. This finalizer needs to be something like C’s free. In Rust, we can actually “free” the memory in the Box using Rust’s automatic memory management:

#[no_mangle]
pub extern "C" fn signature_free_public_key(_: Box<signature::PublicKey>) {}

By taking back ownership of the Box, the Rust side will automatically free the memory too.

In total, the Haskell looks like:

foreign import ccall unsafe "signature_private_key_to_public_key"
  c_signature_private_key_to_public_key :: Ptr Word8 -> IO (Ptr CPublicKey)

foreign import ccall unsafe "&signature_free_public_key"
  c_signature_free_public_key :: FinalizerPtr CPublicKey

privateToPublic :: PrivateKey -> PublicKey
privateToPublic priv = privToPubIO priv |> unsafePerformIO |> PublicKey
  where
    privToPubIO :: PrivateKey -> IO (ForeignPtr CPublicKey)
    privToPubIO (PrivateKey privBS) =
      unsafeUseAsCStringLen privBS
        <| \(privPtr, _) -> do
          pubPtr <- c_signature_private_key_to_public_key (castPtr privPtr)
          newForeignPtr c_signature_free_public_key pubPtr

And you have more and more plumbing for all the other functions.

Is this tedious? Yes. Is it fun? Also, yes. So far, I don’t regret writing the Cryptography in Rust, and I think it will scale easily to the rest of the project. It’s probably a good way to bring good Cryptography to the Haskell ecosystem too. I’m very bullish on the future of Rust as a solid foundation for Cryptographic implementations.

Simulation based Security

I don’t really have anything interesting to say about this for now, other than that I’ve been reading Yehuda Lindell’s How To Simulate It paper, which goes over this technique for proving security. I think I’ve grokked most of the technique, but I need to go over practical applications of it, like for Threshold ECDSA protocols, and see more examples of how to actually prove things secure.

When I was learning game based security 6 or so months ago, it took a lot of examples and “street fighting” using the methodology before I was really comfortable with it. The abstractions we create are relatively crude approximations of the intuitive interactions and properties we try to capture with them, so the interplay between the intuition of what a proof is, and the mechanics of what the syntax we write actually means can get quite subtle.

I have Pragmatic MPC on my reading list, so that will probably be my next encounter with street fighting using simulation based security.

Cryptographic Foundations

I wrote a post or two tinkering around with a more categorical formulation of basic security games, and I’ve been pretty happy with the results so far. I’ve been taking Serge Vaudenay’s “Advanced Cryptography” course this semester, which goes into the basics of security games (roughly, a subset of what’s in Boneh and Shoup’s book), and it’s been interesting comparing my formalization with the one he uses, as well as trying to reframe the examples we’ve encountered in class with my own.

I’ve had to make a few adjustments this week accordingly. One idea I’ve been toying around with is to simply define the state and message types indexed over $\mathbb{N}$ directly, rather than stopping at some arbitrary $N$. You can encode standard situations like “The adversary makes at most $Q$ queries” by simply setting all the states and messages after a certain point to be trivial. i.e. the adversary has to send empty messages, receives empty responses, and the state of the challenger doesn’t change. This avoids the issue of havint his arbitrary size “N” in your formalization of what a game is.

Another little problem with my formalization is that when doing reductions, I only allowed sending one “message” to the adversary you’re using, before having to send another message back to the challenger. This is awkward for many reductions, but not an essential problem. One way around this is to allow all challengers to accept a “I’m not ready to respond yet” message in place of whatever they would have liked to receive, in which case they reply with something trivial in response. This allows querying your own adversary multiple times before responding back to the challenger with something interesting. You can also modify the reduction framework to explicitly allow a polynomial number of interactions with your own adversary before moving back to the challenger. This is why having an “unlimited” number of states indexed by $\mathbb{N}$ is more convenient too.

But all of these is just hand-wavy speculation, I should really get around to making this more concrete, and see what problems end up arising.

Another interesting result I found relates to the product of ciphers. I had defined what the product $A \times B$ and coproduct $A + B$ of two security games meant, categorically, but I hadn’t thought of any practical application of it. This week, I might have found a practical application.

If you have an encryption scheme:

$$ \begin{aligned} &E : \mathcal{K} \times \mathcal{M} \xrightarrow{R} \mathcal{C}\cr &D : \mathcal{K} \times \mathcal{C} \to \mathcal{M} \end{aligned} $$

Then you can define the sequential composition $E_2 \circ E_1$ with:

$$ \begin{aligned} (E_2 \circ E_1)((k_1, k_2), m) &:= E_2(k_2, E_1(k_1, m))\cr (D_2 \circ D_1)((k_1, k_2), c) &:= D_1(k_1, D_2(k_2, c)) \end{aligned} $$

You can also define the parallel composition $E_1 | E_2$ with:

$$ \begin{aligned} (E_1 | E_2)((k_1, k_2), m) &:= (E_1(k_1, m), E_2(k_2, m)) \end{aligned} $$

(To decrypt, you decrypt both, and check that they’re the same, otherwise returning $\bot$.)

It turns out that sequential composition corresponds to the product of the ciphers, in the sense that:

$$ \text{IND-X}(E_2 \circ E_1) \cong \text{IND-X}(E_1) \times \text{IND-X}(E_2) $$

i.e. the security games for the sequential compositions of the ciphers is isomorphic to the product of their security games.

This means that if $E_2 \circ E_1$ isn’t secure, it means that both $E_2$ and $E_1$ are also not be secure, through a purely categorical proof:

($1$ denotes the game which is trivially winnable, here)

Similarly, we have that the parallel composition of ciphers is isomorphic to their coproduct:

$$ \text{IND-X}(E_1 | E_2) \cong \text{IND-X}(E_1) \times \text{IND-X}(E_2) $$

This implies that if $E_1 | E_2$ is secure, then both $E_1$ and $E_2$ must be secure, through another pithy categorical proof:

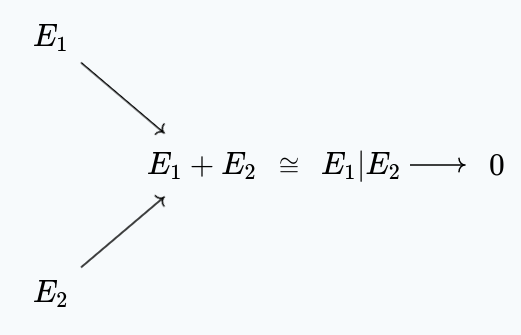
($0$ denotes the game which is unwinnable, here)

I should really write this up more formally, in my notes. I should also get to actually formalizing all of these more concretely, my notes are a bit hand-wavy at the moment. A blog post would be warranted to explain all of this too, but I’d rather get this stuff out there than not.

I’m pretty happy with this little result, and I think this might be the first little success with my experiment.