On Monero's Ring Signatures
Monero is a cryptocurrency which claims to be “private, and decentralized”. One of Monero’s main tools towards this privacy is the ring signature. Ring signatures allow you to sign on behalf of a group, without revealing which member of the group you are. They can be constructed as an elegant extension of Schnorr signatures, and aren’t all that hard to understand either.
The idea behind ring signatures is that you can construct a list of public keys, called a ring, and have any member of the ring able to sign on its behalf, without revealing which member they are.
This lets us obscure our identity to a certain extent: instead of signing a transaction with our identity, we add in additional identities in order to obscure our own.

This is different from a group signature, wherein a group of parties split a private key amongst themselves, and cooperate together to sign on behalf of that group. With ring signatures, we have no affiliation with the other members of the ring. In practice, they’re simply chosen to obscure our own identity.
There are different ring signature schemes, of course, but I’ll be focusing on the variant used in Monero, since those are the ones that piqued my interest recently, and that introduced me the concept.
These signatures are described a bit more completely in Zero to Monero [2], so I’d also recommend readers have a look at that resource as well.
Preliminaries
Let $\mathbb{G}$ be a group of prime order $q$, generated by $G$, and let $\mathbb{F}_q$ be its field of scalars.
Schnorr Signatures
The starting point for this variant of ring signature is the ubiquitous Schnorr signature. Since this scheme has been explained many times, including in this blog, I’ll limit myself to a brief summary.
Key Generation
$$ \begin{aligned} x &\xleftarrow{R} \mathbb{F}_q\cr X &\longleftarrow x \cdot G \end{aligned} $$
Signing
$$ \begin{aligned} \text{sign}(x, m):\cr k &\xleftarrow{R} \mathbb{F}_q\cr K &\longleftarrow k \cdot G\cr e &\longleftarrow H(K, X, m)\cr s &\longleftarrow k + e \cdot x\cr (K, s)& \end{aligned} $$
Verifying:
$$ \begin{aligned} \text{verify}(X, m, (K, s)):\cr s\cdot G &\stackrel{?}{=} K + H(K, X, m) \cdot X \end{aligned} $$
This is “merely” the Fiat-Shamir-ification of a sigma protocol for proving knowledge of the discrete logarithm of $X$.
It’s clear that our verification check is correct as well, given the definition of $s$.
Schnorr Signatures with Hash
With Schnorr signatures, we used the nonce commitment $K$, along with the response $s$ as our signature $(K, s)$. An alternative version of the scheme uses the response $e = H(K, X, m)$ instead of the commitment $K$, making the signature $(e, s)$ instead:
Signing
$$ \begin{aligned} \text{sign}(x, m):\cr k &\xleftarrow{R} \mathbb{F}_q\cr K &\longleftarrow k \cdot G\cr e &\longleftarrow H(K, X, m)\cr s &\longleftarrow k - e \cdot x\cr (e, s)& \end{aligned} $$
Verifying:
$$ \begin{aligned} \text{verify}(X, m, (e, s)):\cr e &\stackrel{?}{=} H(s\cdot G + e \cdot X, X, m) \end{aligned} $$
This scheme is correct, because:
$$ s \cdot G + e \cdot X = (s + ex) \cdot G = k \cdot G = K $$
As for security, notice that we have these mappings:
$$ \begin{aligned} (K, s) &\longrightarrow (H(K, X, m), s)\cr (s \cdot G + e \cdot X, s) &\longleftarrow (e, s)\cr \end{aligned} $$
This naturally implies security reductions between these two signature schemes. A full proof is left as an exercise to the reader 😉.
SAG
The next scheme is a simplification of the one proposed in [1], called Spontaneous Anonymous Group signatures (SAG). This is the first signature scheme that qualifies as a ring signature. Instead of having a single public key used to verify, we instead have an entire ring of public keys. The signer’s key is hidden somewhere in that ring, but the signature does not reveal where the signer’s key is. We don’t need to know anything about the public keys in the ring to create a signature for it, we just need a private key for one of the elements of the ring.
Formally, we have a ring $\mathcal{R} = \{X_1, \ldots, X_n\}$ of public keys. We also have a secret index $\pi \in \{1, \ldots, n\}$, where our public key $X_\pi$ is located. We also have a secret key $x_\pi$, satisfying:
$$ x_\pi \cdot G = X_\pi $$
as with previous schemes.
Signing:
Generate:
$$ \begin{aligned} &k \xleftarrow{R} \mathbb{F}_q\cr &r_i \xleftarrow{R} \mathbb{F}_q \quad (i \neq \pi) \end{aligned} $$
Then calculate:
$$ e_{\pi + 1} \longleftarrow H(\mathcal{R}, m, k \cdot G) $$
and then calculate all the other challenges for $i \in \{1, \ldots, N\}$, starting from $\pi + 1$, and wrapping around:
$$ e_{i + 1} \longleftarrow H(\mathcal{R}, m, r_i \cdot G + e_i \cdot X_i) $$
And finally, we close the ring by setting:
$$ r_\pi \longleftarrow k - e_\pi x_\pi $$
(Notice that this makes $k = r_\pi + e_\pi x_\pi$.)
Our signature is:
$$ (e_1, r_1, \ldots, r_n) $$
Verifying:
Given a signature $(e_1, r_1, \ldots, r_n)$, we re-calculate the challenges: $$ e'_{i + 1} \longleftarrow H(\mathcal{R}, m, r_i \cdot G + e_i \cdot X_i) $$ wrapping around from $n \to 1$.
We then check: $$ e'_1 \stackrel{?}{=} e_1 $$
Why this works
Intuitively, this works because a valid signature satisfies:
$$ e_{i + 1} = H(\mathcal{R}, m, r_i \cdot G + e_i \cdot X_i) $$
The difficulty in forging this signature comes from the recursive, or wraparound nature of this chain of values:
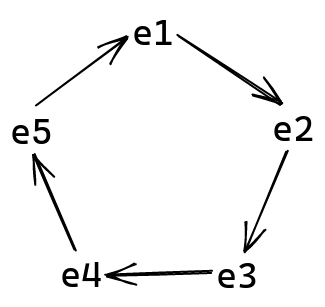
Verifiers of the signature observe this circle as a whole. The signer, on the other hand, creates the ring starting from their secret index $\pi$, in a linear fashion. Then, they use their knowledge of $x_\pi$ in order to “tie” the ring together, creating the recursive link:
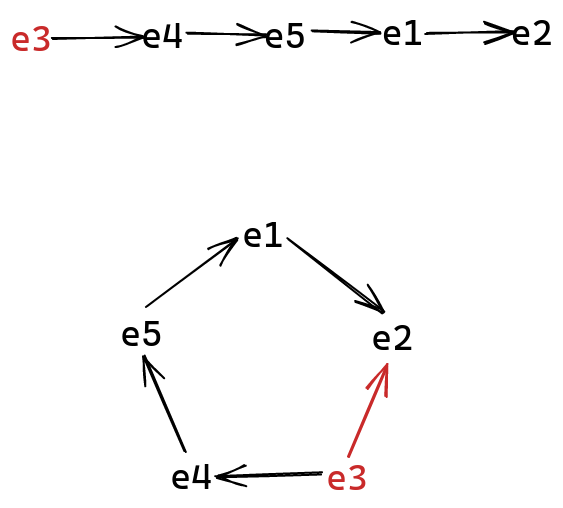
Since the ring is treated as a whole, there’s no way to figure out which index $\pi$ the signer had.
Linkability
In the context of Monero, ring signatures are used to sign transactions. More specifically, you can think of coins with different amounts having public keys, which can be used to authorize spending them. With a ring signature, you can hide which coin you’re actually spending, by dissimulating it among many others.
One problem with this hiding is that you could potentially spend the same coin twice, since you wouldn’t be able to tell that the same coin was used twice as the hidden part of a ring. This is a classic “double-spend” attack.
We want to be able to add some kind of tag to our signatures to detect this duplication. This property is called linkability. It allows us to link different ring signatures together, so that we can tell if the same output gets spent twice. Naturally, we don’t want to reveal which output of the ring this is either.
bLSAG
This brings us to Back’s Linkable Spontaneous Anonymous Group signatures (bLSAG), as described in [3]. The core idea is to augment signatures with a key image, which should be the same whenever a private key is used to make a ring signature.
We also need a hash function $\mathcal{H} : \{0, 1\}^* \to \mathbb{G}$, hashing messages directly to points, without knowing the discrete logarithm.
Signing:
First, calculate a key image:
$$ \tilde{X} = x_\pi \cdot \mathcal{H}(X_\pi) $$
Then generate:
$$ \begin{aligned} &k \xleftarrow{R} \mathbb{F}_q\cr &r_i \xleftarrow{R} \mathbb{F}_q \quad (i \neq \pi) \end{aligned} $$
Then compute challenges:
$$ e_{\pi + 1} \longleftarrow H(\mathcal{R}, m, k \cdot G, k \cdot \mathcal{H}(X_\pi)) $$
and
$$ e_{i + 1} \longleftarrow H(\mathcal{R}, m, r_i \cdot G + e_i \cdot X_i, r_i \cdot \mathcal{H}(X_i) + c_i \tilde{X}) $$
Finally, close the ring by defining:
$$ r_\pi \longleftarrow k - e_\pi x_\pi $$
Our signature is then $(c_1, r_1, \ldots, r_n)$, along with the key image $\tilde{X}$.
Verifying:
Verification proceeds similarly to the SAG case.
We recompute the challenges:
$$ e'_{i + 1} \longleftarrow H(\mathcal{R}, m, r_i \cdot G + e_i \cdot X_i, r_i \cdot \mathcal{H}(X_i) + c_i \tilde{X}) $$
and check that:
$$ e'_1 \stackrel{?}{=} e_1 $$
Linkability
The key image lets us tie to different ring signatures produced with the same private key together. If we use the same $x_\pi$ twice, we’ll have the same key image $\tilde{X}$. The key image is also integrated into the loop of challenges, which keeps signers honest in terms of linkability: they can’t try and avoid linking their signatures, even if they use different rings.
Note that it’s very important that the hash function $\mathcal{H}$ returns points in $\mathbb{G}$ without revealing their discrete logarithm. If we have $\mathcal{H}(m) = h(m) \cdot G$, we would have:
$$ \tilde{X} \longleftarrow x_\pi \cdot \mathcal{H}(X_\pi) = x_\pi \cdot h(X_\pi) \cdot G = h(X_\pi) \cdot X_\pi $$
This means that we could iterate over all of the $X_i$ in the ring $\mathcal{R}$, and check:
$$ h(X_i) \cdot X_i \stackrel{?}{=} \tilde{X} $$
in order to find which member of the ring produced this signature. Having the hash function return a point in the group directly avoids this issue.
Aside from the addition of the key image, this signature protocol is the same as the SAG scheme we saw before.
MLSAG
I briefly touched upon the model of transactions in the context of Monero. Essentially, coins have different values, and come with public keys. Owning a coin means knowing the private key associated with it, and spending that coin involves signing a transaction using that key. In practice, you often want to spend multiple coins in the same transaction, in the same way that you might pay for something using multiple bills from your own wallet. While you could do this by producing one ring signature for each coin you want to spend, it’s more efficient to combine this signatures into a single, more compressed signature, as shown in [3]. This scheme is called Multilayer Linkable Spontaneous Anonymous Group signatures (MLSAG).
Instead of a single key-pair $x_\pi, X_\pi$, we now have an entire column of these key-pairs $x_\pi^j, X_\pi^j$ (for $j$ in some indexing set). Instead of a simple ring $\mathcal{R} = \{X_i\}$, a row of public keys, our ring is now an entire matrix $\mathcal{R} = X_i^j$. Our public key is hidden as a column $X_\pi^j$ of this matrix.
For linkability, we want to be able to detect if any of the $x_\pi^j$ are reused between signatures. This naturally corresponds with wanting to detect if a coin was spent multiple times across different transactions.
Signing:
First, we calculate key images:
$$ \tilde{X}^j \longleftarrow x_\pi^j \mathcal{H}(X_\pi^j) $$
Then we generate random numbers:
$$ \begin{aligned} &k_j \xleftarrow{R} \mathbb{F}_q\cr &r_i^j \xleftarrow{R} \mathbb{F}_q & \end{aligned} $$
Then we generate the first challenge:
$$ e_{\pi + 1} = H(\mathcal{R}, m, \{k_j \cdot G\}, \{k_j \cdot \mathcal{H}(X_\pi^j)\}) $$
And then generate the next challenges, wrapping around, as usual:
$$ e_{i + 1} = H(\mathcal{R}, m, \{r_i^j \cdot G + e_i \cdot K_i^j\}, \{r_i^j \cdot \mathcal{H}(X_\pi^j) + e_i \tilde{X}^j \}) $$
And finally, we close the loop by setting:
$$ r_\pi^j \longleftarrow k_j - e_\pi x_\pi^j $$
Our signature is then:
$$ (e_1, \{r_i^j\}) $$
along with the key images $\tilde{K}^j$.
Verification:
We recalculate the key challenges:
$$ e'_{i + 1} = H(\mathcal{R}, m, \{r_i^j \cdot G + e_i \cdot K_i^j\}, \{r_i^j \cdot \mathcal{H}(X_\pi^j) + e_i \tilde{X}^j \}) $$
And then check that:
$$ e'_1 \stackrel{?}{=} e_1 $$
Intuition
This scheme is a straightforward extension of bLSAG, using multiple keys at the same time. One advantage over a naive duplication is that only need to send one challenge $e_1$, instead of $M$ challenges, if we were to simply produce $M$ ring signatures. This is very important on the context of Monero, and cryptocurrencies, since reserving space on the digital ledger is very expensive, so having the smallest transactions possible is ideal. I should also note that Monero has a perverse tradeoff between privacy and cost here. A larger ring size makes for a larger signature, and thus a larger transaction fee, but also more privacy.
Notes on Thresholdization
We use our private keys $x_\pi^j$ only in a linear fashion. We never multiply them together, but instead act on them with other integers, or use them to act on a scalar. Because of this, if our keys were split between multiple parties in a linear fashion as:
$$ x_\pi^j = \sum_k \ _k x_\pi^j $$
it would still be easy for the different parties to collaborate, and produce a signature for these keys, without revealing their share to any other party.
This naturally extends to the cast of an arbitrary threshold of parties, by using polynomial secret sharing.
Conclusion
Most of this information can be found in [2], but hopefully this post could provide a bit more intuition about the clever tricks going into these signature schemes.
I believe Monero has recently moved on to use CLSAG [4], which is a variant of the MLSAG scheme, but with weaker linkability properties. Frankly, I don’t understand how those weaker linkability properties are worked around in practice with transactions, so I refrained from including them in this presentation.
The way these signatures are assembled into an actual private transaction scheme is quite interesting actually, and can be found in [2], once again.
References
[2] koe, Kurt M. Alonso, Sarang Noether, Zero to Monero
[3] Shen Noether, Adam Mackenzie, and Monero Core Team, Ring Confidential Transactions