Recently, I’ve been working on a little encryption tool called Nimotsu. My goal with this project was to implement all of the cryptographic primitives involved. I had a lot of fun doing so, and thought it would make for an interesting blog post.

Note that I’m not advocating the use of this application over other alternatives. I made this app for my learning and entertainment, so use a battle-tested application instead.

The Application

Nimotsu lets you encrypt data to someone else, given their public key, such that only they can decrypt that data. (Of course, since you encrypted the data in the first place, you would also know what it decrypts to, but that’s beside the point).

To use Nimotsu, you’d first generate a key-pair:

→ nimotsu generate --out key.txt                                
Public Key:
荷物の公開鍵089F9CFDF80C7EFCCDE2BFAE73677C2567AD3C398AF93B1D505D9D788E4DB078

Now, the file key.txt contains your private key, and looks like this:

# Public Key: 荷物の公開鍵089F9CFDF80C7EFCCDE2BFAE73677C2567AD3C398AF93B1D505D9D788E4DB078
荷物の秘密鍵4036684A2C4DC2FC195E0FE53F17A90FA3CFAAF70708F5373E263582200D4027

If someone wanted to send you a cute cat picture, they can do that using your public key:

→ nimotsu encrypt cat.png --out encrypted.bin
  --recipient 荷物の公開鍵089F9CFDF80C7EFCCDE2BFAE73677C2567AD3C398AF93B1D505D9D788E4DB078

They would then send you the file encrypted.bin. Since you have your private key, you (and only you) can decrypt the file:

→ nimotsu decrypt encrypted.bin --out cat.png --key key.txt

And that’s about it! This is a very simple application. The concept is pretty old-school, and surpassed by various more practical and more secure programs, but I wanted a simple project to let me implement some of the primitives involved.

The Protocol

So, what primitives does this program use? Let’s have a closer look at how the protocol for encrypting data works.

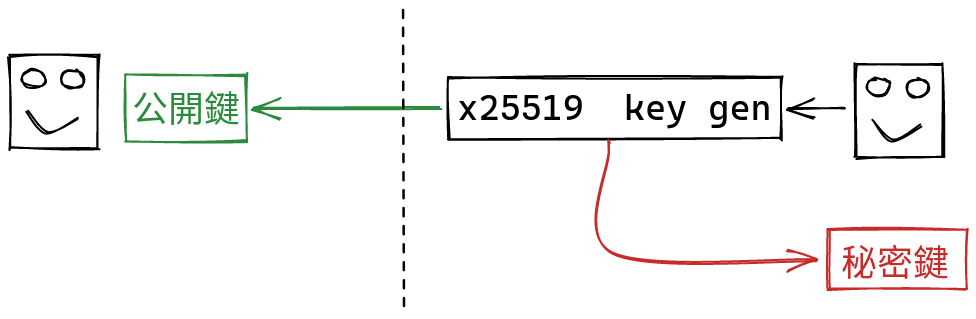
A nimotsu key pair is just an x25519 key pair. You generate a public key, that you share with others, and a secret key, that you keep to yourself:

When someone wants to send you a file, they first generate a new key pair, and send you the public part. We call this key pair “ephemeral”, because it only gets used this one time. Using your public key, and the secret key they’ve just generated, they can use the x25519 function to derived a shared secret. On your side, you can combine your secret, and the public key they’ve just sent you, and derive the same secret!

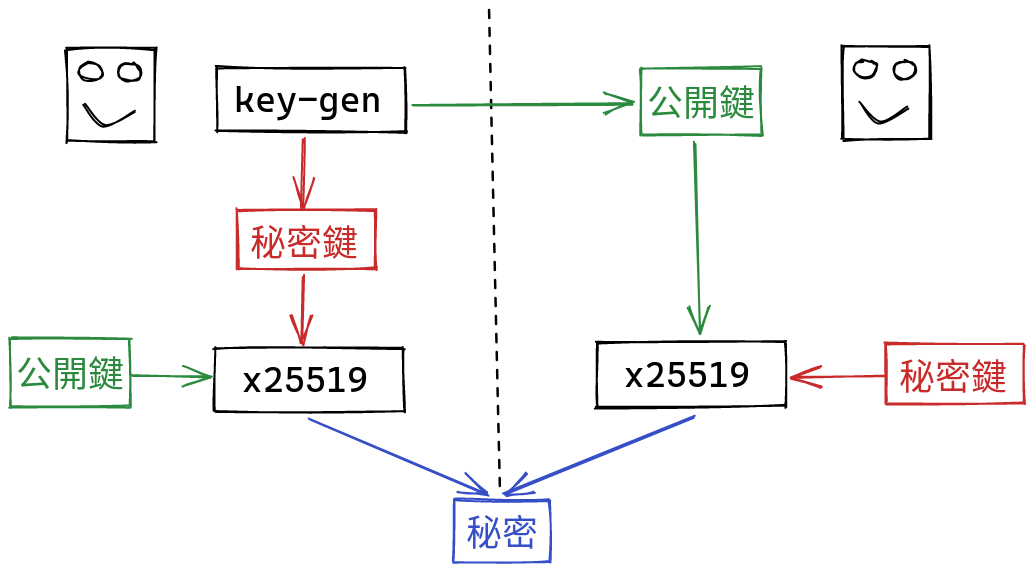
The beauty of public key cryptography is that you’ve managed to derive a shared secret, while only communicating public data to each other!

From this shared secret, we derive a symmetric key using Blake3. We can then encrypt and authenticate data using ChaCha20-Poly1305:

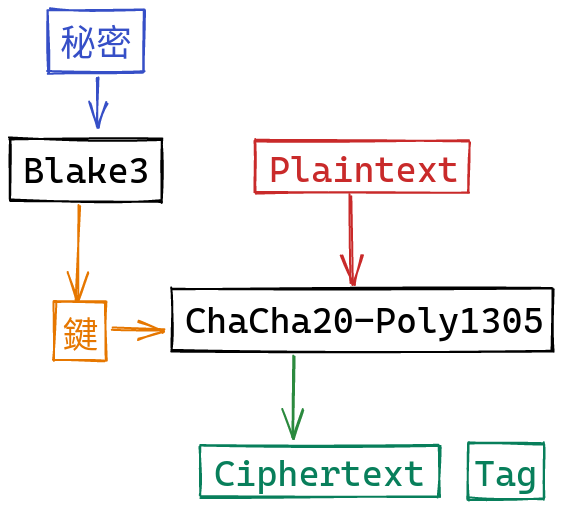
On your end, you can derive the same key, and use that to decrypt the data, and ensure that it wasn’t tampered with. And that’s about it!

This protocol is pretty simple. Essentially, it’s just ECIES. The fun part was implementing it!

Implementation

I decided to implement the application in Rust; I like Rust. There are plenty of crates I could use for each of these primitives, but my whole reason to make this application was to have an excuse to implement all of them from scratch!

I learned quite a bit by implementing these primitives, and hopefully can illustrate some of the interesting aspects involved.

Curve25519

I initially started this project out of a budding interest in Elliptic Curve Cryptography. Since I learn new concepts best by implementing them, I wanted an excuse to implement some ECC myself. Curve25519 is a very popular curve, designed to be easy to implement in a constant-time fashion. Timing attacks being another interest of mine, and already being a Daniel J. Bernstein fanboy, I had no choice but to use x25519 (the diffie hellman variant of Curve25519, the actual Elliptic Curve) for the key exchange component!

Curve25519 is an Elliptic Curve (Montgomery, specifically) defined by the following equation:

$$ y^2 = x^3 + 48862 x^2 + x $$

over the prime field of numbers modulo $p = 2^{255} - 19$. Because of the Montgomery shape, there’s a neat constant-time way of doing scalar multiplication of points on the curve, which is the key operation needed to implement the x25519 function, as we’ll see later.

Arithmetic Modulo $2^{255} - 19$

Because of the specific structure of this prime number, there are a few interesting tricks to optimize implementation of modular arithmetic. I’d recommend having a look at the arithmetic.rs file if you want all of the details of how the implementation works.

That basic strategy I went with was to represent numbers in $\mathbb{F}_p$ over 4 limbs of 64 bits:

pub struct Z25519 {
    pub limbs: [u64; 4],
}

This gives us 256 bits in total, which is actually enough to hold the addition of two elements, since that’s at most:

$$ 2 \cdot (p - 1) = 2^{256} - 40 < 2^{256} $$

Another strategy is to use unsaturated limbs, of only 51 bits. 5 limbs of 51 bits each aligns exactly with 255, which is convenient. There are several reasons to use unsaturated limbs. One is not having to rely on intrinsics like adc. Another is making Montgomery multiplication more efficient, by requiring fewer registers. Ultimately, I went with saturated limbs out of familiarity, and simplicity. Conversion to 64 bit limbs from bytes is a lot easier, for example.

Intrinsics

When adding multiple limbs together, we need to add them limb-by-limb, making sure to propagate the carry produced at each step:

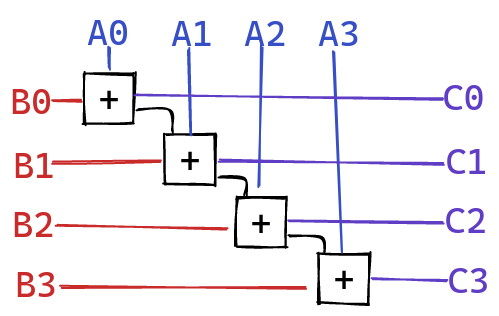
Fortunately, ISAs usually come with a convenient adc instruction, which adds two 64 bit numbers together, along with a carry from a previous step. We can chain multiple adcs together to implement our addition.

To use this intrinsic on the x86_64 isa, we can use feature gating:

pub fn adc(carry: u8, a: u64, b: u64, out: &mut u64) -> u8 {
    #[cfg(target_arch = "x86_64")]
    {
        unsafe { arch::_addcarry_u64(carry, a, b, out) }
    }
    #[cfg(not(target_arch = "x86_64"))]
    {
        let full_res = u128::from(a) + u128::from(b) + u128::from(carry);
        *out = full_res as u64;
        (full_res >> 64) as u8
    }

If this intrinsic isn’t available, we fall back on using u128. Using u128 is slightly slower than using the adc instruction directly, unfortunately.

For subtraction, we need a similar operation, sbb. This subtracts one 64 bit number from another, along with a borrow bit. We can use feature gating once more to use the intrinsic when available:

pub fn sbb(borrow: u8, a: u64, b: u64, out: &mut u64) -> u8 {
    #[cfg(target_arch = "x86_64")]
    {
        unsafe { arch::_subborrow_u64(borrow, a, b, out) }
    }
    #[cfg(not(target_arch = "x86_64"))]
    {
        let full_res = i128::from(a) - i128::from(b) - i128::from(borrow);
        *out = full_res as u64;
        u8::from(full_res < 0)
    }
}

Once again, we fallback on using 128 bit numbers, this time with i128.

The availability of u128 in Rust is also convenient for multiplying two 64 bit numbers together, producing a 128 bit number.

Modular arithmetic and Constant Time Operations

Addition and subtraction are the fundamental building blocks for arithmetic in $\mathbb{F}_p$, but we still need to do reduction modulo $p$ after calling these primitives.

After an addition, our value is at most:

$$ 2p - 2 $$

With a single subtraction of $p$, we get $p - 2$, which is in range. So, to do modular addition, we do normal addition, and then subtract $p$ if necessary. We need to subtract $p$ if our number is $\geq p$. We can check this by performing the subtraction, and seeing if an underflow happened, by looking at the last borrow. We can then keep this result if there’s no borrow.

One problem is that you shouldn’t use an if statement to check this condition and select the right result. This is because of timing side-channels. Essentially, not only will doing the subtraction take more time, but the branch predictor itself can be oberved to see which branch was taken. Because of this, you instead always write down a result, but use bitwise operations to make the selection process completely opaque.

Thankfully, there’s a nice crate called subtle which provides basic primitives for constant-time operations, and I’ve made heavy use of this crate for implementing arithmetic.

One nice primitive provided by this library is a conditional_select function for various types. This allows us to choose between two alternatives, based on a condition, without leaking the value of that condition.

This function is already implemented for u64, and we can build off of that implementation for our Z25519 type as well:

impl ConditionallySelectable for Z25519 {
    fn conditional_select(a: &Self, b: &Self, choice: Choice) -> Self {
        Z25519 {
            limbs: [
                u64::conditional_select(&a.limbs[0], &b.limbs[0], choice),
                u64::conditional_select(&a.limbs[1], &b.limbs[1], choice),
                u64::conditional_select(&a.limbs[2], &b.limbs[2], choice),
                u64::conditional_select(&a.limbs[3], &b.limbs[3], choice),
            ],
        }
    }
}

We can then implement modular addition between $x$ and $y$ by adding them, to get $z = x + y$. Then we calculate $z - m$, and select between $z$ and $z - m$ based on whether our first addition produced a carry, and whether our subtraction produced a borrow. The subtraction is always calculated, and the selection is performed without leaking the value of this condition. Our modular addition routine is thus constant-time.

Folding Large Results

For modular addition and subtraction, our result is small enough that a conditional addition or subtraction of $p$ is enough to reduce it.

For larger results, like after a scaling, or a multiplication, this doesn’t suffice. Thankfully, we can use the special structure of $p$ to reduce this values faster than for a generic modulus.

Scaling

One useful operation is multiplying a multi-limb number $x$ by a single-limb factor $\alpha$. Since $x < 2^{255}$, we can write the result as:

$$ \alpha \cdot x = q \cdot 2^{255} + r $$

Now, since $p = 2^{255} - 19$, we see that $2^{255} \equiv 19 \mod p$. We can then rewrite our result as:

$$ \alpha \cdot x \equiv 19q + r \mod p $$

The value $19q$ fits over two limbs, so we can use our standard modular addition routine.

Multiplication

After multiplying two field elements $x$ and $y$, we end up with a number that fits over 8 limbs, which we can write as:

$$ xy = a \cdot 2^{256} + b $$

with $a, b < 2^{256}$. Using the structure of $p$, we note that $2^{256} \equiv 38 \mod p$. This means that our multiplication is nothing more than:

$$ xy \equiv 38a + b \mod p $$

We can calculate this result by combining the scaling operation we defined earlier, and a modular addition.

There are probably faster ways to do multiplication, but I settled on these simple optimizations.

x25519

To define the x25519 function, we use our elliptic curve: $$ C: y^2 = x^3 + 48862x^2 + x $$ defined over the prime field $\mathbb{F}_p$, with $p = 2^{255} - 19$. We’ve already seen a bit of how $\mathbb{F}_p$ is implemented, so now we can look at how the curve is used.

The x25519 function uses scalar multiplication. This takes a scalar $s \in \mathbb{Z}$, and a point $P \in C(\mathbb{F}_p)$, and then computes:

$$ s \cdot P := \sum_{i = 1}^s P $$

using the point addition formula defined on this curve.

We can use this to create a key exchange system, using ECDH. We choose a basepoint $G$, and then work in the group $\langle G \rangle$ generated by this point. For x25519, this basepoint is:

$$ (9, \sqrt{39420360}) $$

A private key is a scalar $s \in \mathbb{Z}/q \mathbb{Z}$, where $q$ is the order of $G$ (this is $\approx 2^{252}$). The corresponding public key is the point $P = s \cdot G$. It is widely believed that recovering $s$ from $P$ is exceedingly difficult. (This problem is the infamous ECDLP (Elliptic Curve Discrete Logarithm Problem)).

Two key pair holders with $(s_1, P_1 = s_1 \cdot G)$ and $(s_2, P_2 = s_2 \cdot G)$ can calculate a shared secret, only using each other’s public key. The first person calculates $$ s_1 \cdot P_2 $$ and the second calculates $$ s_2 \cdot P_1 $$

they then both end up with the shared secret:

$$ s_1s_2 \cdot G = s_2s_1 \cdot G $$

Implementation

In theory, all we need to implement x25519 is a routine for scalar multiplication.

The first divergence from this theory is that we only actually need the $x$ coordinate of our points.

Another interesting quirk is that our scalars are not uniformly in $[0, q - 1]$. Instead, we generate a random number in $[0, 2^{256}]$, fitting over 32 bytes, and then use a special clamping procedure:

scalar[0] &= 248;
scalar[31] &= 127;
scalar[31] |= 64;

This clamping clears the lowest 3 bits, and sets the highest 2 bits to $01$.

Clearing the lowest 3 bits ensures that our scalar $s$ is a multiple of $8$. This is because the number of points on the curve is actually $8 \cdot q$. We say that $8$ is the cofactor for this curve. When we use scalar multiplication with a point outside of $\langle G \rangle$, having a scalar that’s a multiple of $8$ ensures that the result is $\mathcal{O}$, which prevents leaking information about our scalar.

Setting the top bits ensures that we have a high order point, and was also designed to mitigate certain implementations varying in time based on the number of leading zero bits, by making this number fixed.

To implement scalar multiplication, the rough idea is to use binary exponentiation. Esentially, we do:

R = O
for b in s.msb..s.lsb:
    R = 2 * R
    if b == 1:
        R = R + P

One way of seeing this is correct is by writing $R = v \cdot P$ at each step, and then seeing how the exponent $v$ is modified throughout this routine. At the end of the routine, we want $v = e$. We accomplish this by shifting each bit of $e$ into $v$, from top to bottom. At each iteration, we need to shift $v$ left by one bit, doubling it, and thus doubling $R$ as well. If the next bit of $e$ is set, then we need to add $1$ to $v$, and thus add $P$ to $R$. By the end, we have $R = e \cdot P$.

Of course, checking this bit is actually not constant time. It would also seem like we need a routine for adding any two points, but we can streamline this quite a bit.

The technique for streamlining this scalar multiplication, making it both fast, and constant-time, is called the Montgomery Ladder, and I’ve written some detailed notes about how it works. I don’t think the details are all that interesting for this post.

Blake3

After deriving a shared secret, we can use this secret to create a symmetric encryption key. The usual way to do this is to use some kind of KDF. This takes in some random data, and then generates a secret key using that data. This isn’t strictly necessary, but is a good practice.

For this KDF, I went with Blake3, mainly because it was shiny and new, but also because I liked how it had a unified structure for different hashing modes, including key derivation. I implemented all of this in blake3.rs.

The neat thing about Blake3 is that it splits the data it needs to hash into many chunks, and then organizes those chunks into a tree. This tree structure is is essentially a Merkle Tree, and enables parallelizing the hash.

Unfortunately, I didn’t actually need to use this neat functionality, because I only ever use Blake3 as a KDF over a tiny amount of data. This means that I’ll have to actually implement all of Blake3 some other time, in order to learn how it works!

The basic idea behind Blake3 is pretty simple. You first split your data into individual blocks of 64 bytes. For each block, you initialize a state using different values based on the context. One of these values is used to ensure that this state depends on the hash of previous blocks, another assigns a different counter value for different blocks, another distinguishes between different uses of the hash, etc. Then, this state is mixed around, guided by the message data inside of the block. You do several rounds of mixing, each time permuting the message data as well.

This makes it so that a small change in the initial state, or a small change in the message, leads to a large difference in the output state. This ouptut state can then be used as a hash value.

To derive a key, we essentially hash both a context string, and the key material itself:

$$ H(\text{ctx} || m) $$

This makes it so that different contexts produce different keys from the same material. Blake3 also uses domain separation, so using the hash in KDF mode will produce a different value than actually hashing the context string and then the material.

ChaCha20-Poly1305

Armed with a symmetric key, we can use it to encrypt our data. Not only do we want to encrypt it, but we also want to make sure that our data can’t be tampered with. The classical approach is to encrypt the data, and then use some kind of HMAC to ensure its integrity. The more modern approach is to use a dedicated AEAD mode for a cipher, which provides encryption and authentication in one nice package.

The AEAD mode of choice for me is ChaCha20-Poly1305. I like this AEAD over AES, because I think stream ciphers are more elegant than block ciphers, and I like the constant-time friendliness of ChaCha20.

I implemented this AEAD mode in chacha20.rs.

ChaCha20

As mentioned previously ChaCha20 is a stream cipher. The idea is to generate a random stream of data $s$ the same length as our message $m$, then calculate our ciphertext as:

$$ c = s \oplus m $$

If $s$ were truly random, then this would be unbreakable. Of course, $s$ is not perfectly random, but rather generated using the entropy contained inside of our symmetric key, and our nonce. But, if we can use these two pieces of entropy to extend them into a stream opaquely, then we can provide a very good cipher.

Generating this stream is actually done in a way similar to how Blake3 works. We generate our stream by blocks of 64 bytes. We initialize a state using our two sources of entropy, our key and nonce, as well as a counter for the block. We then mix up this state, so that the entropy diffuses through the state. There’s an avalanche effect, where a small change, like with the counter, results in a very large change in the final state. We do this with 20 rounds in a row, each of which is actually extremely similar to a round in Blake3. This is why it’s called ChaCha20.

This is simple, elegant, fast, and constant-time. What’s not to like?

Poly1305

ChaCha20 allows us to encrypt our data, and Poly1305 allows us to make sure that our data can’t be tampered with at all. The idea is to use a onetime key split into two 16 byte parts $(r, s)$. These parts can be derived from our key and nonce, but that’s part of the AEAD construction, not Poly1305 itself.

The idea is to work in the field $\mathbb{F}_p$, with $p = 2^{130} - 5$. We treat our message as a polynomial $m \in \mathbb{F}_p[X]$, we can then calculate an authentication tag as:

$$ m(r) + s \mod p $$

If the message is different, then our authentication tag will change as well. Forging this authentication tag should be extremely difficult without knowing both $r$ and $s$. This ensures the authenticity of our message.

To construct an AEAD mode from this, we create an authentication tag over the encrypted data provided by ChaCha20.

Further Work

While the tool works, there are still a few features that would be nice to have. One feature would be implementing passphrase protection over the private key file. This would involve using a password hash, like Argon2, to generate a symmetric key, used to encrypt the private key file, instead of storing it in the clear.

Another cool feature, mainly for learning purposes, would be to implement different curves for the exchange, instead of just Curve25519. I kind of want to play around with binary field curves, since those use a fundamentally different kind of arithmetic.

Conclusion

As a reminder, Nimotsu is a little application to encrypt a file to someone, using their public key, and you might have some fun using it, and even more fun reading its source code.

This post wasn’t really trying to provide a complete introduction to the various algorithms involved, but rather to talk a bit about this little tool I’ve been working on. I should probably actually take the time to explain how these primitives work in greater detail.