Constant-Time Big Numbers: An Introduction
Over the past couple months, I’ve been working on a library for constant-time Big Numbers in Go. I think it’s about time that I presented a bit of this work.
In this post, I’ll try to explain what exactly this work is about, and why you might care about it. This post is intended to be an introduction, and shouldn’t require any background in Cryptography.
What are Big Numbers?
As the title suggests, the main concept here is a “Big Number”. Essentially, Big Numbers are nothing more than a way to program with arbitrarily large integers.
The usual integers you use
in programming have a fixed size. Big Numbers,
on the other hand, have to be dynamically sized.
For example,
a uint64 type represents integers from $0$ up to $2^{64}$, consuming
$64$ bits of memory. A Big Natural Number type would instead be able
to represent all numbers in $\mathbb{N}$. This requires a type that grows
in size to represent larger numbers.
Big Numbers are familiar
Big Numbers are actually a familiar concept. As programmers, we’re used to working with fixed size integers. This is an acquired taste. The natural way you’d think about numbers isn’t constrained in this way. Most people don’t see numbers as having an arbitrary upper bound; numbers seem to go on forever:
$$ 0, 1, 2, 3, \ldots, 18446744073709551619, \ldots $$
That last number is actually too big to fit over 64 bits, yet it seems perfectly natural at a first glance.
Essentially, a Big Number library provides a way to work with these arbitrarily large numbers, providing the common operations, like addition, multiplication, etc.
Limited hardware size
CPUs already include operations for working with fixed size integers. Nowadays, the most common register size is 64 bits. This means that operations on integers up to $2^{64}$ are going to be possible in hardware. However, if you want to work with numbers larger than 64 bits (or whatever your register size happens to be), you’ll need to have an extra software layer implementing this abstraction.
Increasing the size of the CPU’s registers can’t help either, since Big Number support requires supporting arbitrarily large numbers, in general.
Schoolbook arithmetic
Not only are Big Numbers familiar to us, but so are the algorithms manipulating them. To implement operations on Big Numbers, you start with the pen-and-paper recipes you learned back in grade-school.
We usually work with numbers in base 10. This means that we interpret a sequence of digits, such as:
$$ 1234 $$
as the product of each digit with the matching power of 10:
$$ 1 \cdot 1000 + 2 \cdot 100 + 3 \cdot 10 + 4 \cdot 1 $$
We could emphasize that we’re taking powers of 10 here, writing this number as:
$$ 1 \cdot 10^3 + 2 \cdot 10^2 + 3 \cdot 10^1 + 4 \cdot 10^0 $$
To add two numbers on pen and paper, you first line them up:

and then you add the digits one by one, making sure to keep track of any carry generated by an addition:

A carry happens when two digits add up to something greater than 9. For example, $5 + 7 = 12$.
Multiplication uses a similar method, where you first multiply one number by each digit of the other, shifted with the right number of zeros:

And then, you add all of these terms together:
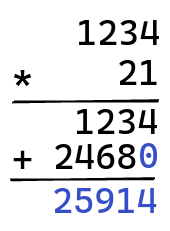
There are pen-and-paper algorithms to implement all of the operations on big numbers, and these serve as the foundation for a library programming these up.
Digits, bits, and limbs
Conceptually, I like thinking of big numbers as being large decimal numbers, like:
$$ 43707 $$
We could also express this number in an alternate base. In base 2, this would be:
$$ 1010101010111011 $$
In base 16, or hexadecimal, this would be:
$$ AABB $$
In base 10, we usually refer to each individual component of a number as a “digit”. In base 2, these become “bits”, and in base 16, I guess you would call these “nibbles” (being 4 bits long), but I haven’t really used that terminology.
In practice, you want to represent your big numbers using a much larger base. Typically, you’d want each component of your number to use an entire CPU register. This means representing numbers in base $2^{m}$ (where $m$ is your register width). With components this big, we usually call these “limbs”: wordplay on “digits”, of course.
The foundation for working with Big Numbers (at least in the libraries I know of), is thus representing them over a list of individual limbs, making a number over base $2^m$.
Big Numbers in Cryptography
Big Numbers have a natural application when implementing mathematical algorithms: you don’t want to be constrained by the size of your machine integers. In fact, because Big Numbers are arguably more natural, some programming languages use them by default, such as Python.
The application that we’re interested in here is Cryptography. Specifically, public-key Cryptography. The main public-key cryptosystems are actually based on the application of Big Numbers; at least conceptually.
RSA
RSA is perhaps the prototypical example of a public key cryptosystem. I won’t be going over the details of how RSA works; just highlighting a few aspects about how it uses Big Numbers.
You have a public key $(e, N)$ with an exponent $e \in \{0, \ldots, N - 1\}$ and a natural number $N \in \mathbb{N}$. Operations are done modulo $N$ later. Your private key is another exponent $d$.
Typically, you talk about $2048$ or $4096$ bit RSA. This refers to the size of the modulus $N$, in bits. Since you’re working with numbers that are about $2048$ bits long, you need to have support for Big Numbers.
Furthermore, you also need your number library to support modular arithmetic: the operations making up the RSA system work modulo $N$.
Elliptic Curves
With Elliptic Curve Cryptography, you have much more complicated operations as your foundation. When using a prime field, you bulid up these operations using arithmetic modulo $p$, a prime number. Typically, $p$ is going to be 256 bits or so. In this case, you can use Big Numbers, along with the modular arithmetic operations. This only works for prime fields though. For Galois Fields, you need different operations: multiplication is no longer just modular arithmetic.
One advantage of ECC over RSA is that the parameters you’re working with can be chosen well in advance. The curve you’re using is part of the system itself, whereas the parameters in RSA are chosen dynamically. Because of this, it’s possible to handcode operations over a given curve using exactly the right sized numbers, whereas RSA requires using dynamically sized Big Numbers.
Because of this, as well as the relative smallness of the numbers involved, most implementations of ECC opt for doing things in a curve specific way, instead of using a generic Big Number library. The disadvantage is that this requires much more effort to adopt a new curve, since you need to write a new implementation as well.
Timing attacks
So far, we’ve seen what Big Numbers are; now it’s time to see what we mean by “Constant-Time”. The use of Big Numbers in Cryptography is actually what makes us care about being Constant-Time.
Briefly, you can call a program “Constant-Time” when it isn’t vulnerable to “timing attacks”. A timing attack, broadly speaking, is when observing the timing patterns of some program allows an adversary to violate the desired security properties of that program.
For example, if an adversary can infer the value of some secret by observing the execution time of some program using that secret, then that would constitute a timing attack.
When the timing patterns of some program reveal information, we call this a timing side-channel.
A toy example
Let’s take a simple example, to illustrate how this works in practice.
Suppose that you’re an adversary who wants to learn the value of Alice’s password. Alice allows you to submit guesses to her server, which will check your guess, and then tell you whether or not it matches the password.
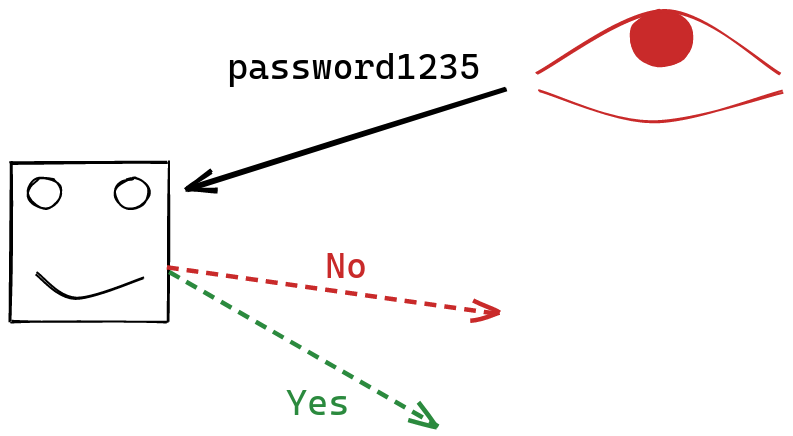
If the password is $b$ bits long, then you’ll need $O(2^b)$ guesses the recover the password, if you just rely on the information provided by the server.
The naive way of comparing strings is actually vulnerable to a timing attack.
The typical way comparison is implemented compares two strings
character by character, returning false as soon as a mismatch is detected:
var password string
func Eq(guess string) bool {
if len(guess) != len(password) {
return false
}
for i := 0; i < len(guess); i++ {
if password[i] != guess[i] {
return false
}
}
return true
}
This short-circuiting behavior provides us with an additional signal! Not only can we observe whether or not our guess was correct, but we can also observe how long it takes the server to respond with an answer. The longer we wait, the more characters are correct at the start of the string. In fact, we can basically figure out how many characters at the start of the string were correct:
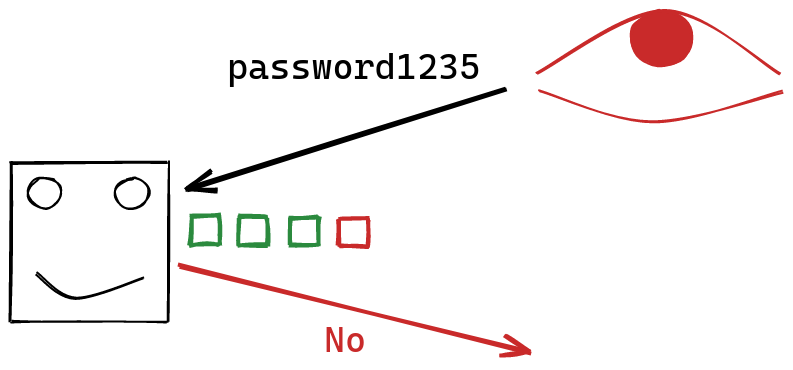
Using this information, instead of trying random strings, we can focus on guessing character by character. At first, none of our characters our correct. Then, we keep changing the first character of our string, until we get to see that it’s correct:

We can keep guessing character by character, since we can observe whether or not each new character was correct, looking at the timing patterns we observe:
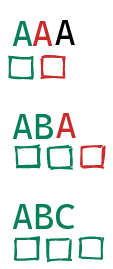
With this in place, we improve our $O(2^b)$ bounds all the way to $O(b)$! Instead of trying all the different combinations, we can instead guess bit by bit, or character by character. This is an exponential improvement, and completely destroys the security of this setup.
More subtle sources
Keep in mind that this is just an example. In practice, such a direct guessing game wouldn’t be in place, nor would you use such an obviously broken comparison routine.
In this example, the number of steps our operation take varies directly, based on its input, because of how we’ve structured it. Timing leaks can be more subtle, however. Code that is ostensibly not variable time can actually hide timing variations arising from the behavior of the hardware. For example, accessing memory can leak addresses through cache timing [2], and conditional statements can leak which branch was chosen, even if both branches take the same amount of time [1].
Incomplete mitigations
If our program has a timing leak, we can first try and hide this leak, instead of attempting to re-write the program completely. Unfortunately, some of the obvious mitigations don’t work, and others only work incompletely.
Sleeping
When I’ve explained timing attacks to other people, the first mitigation they think of is adding a random amount of waiting to the program. If we take the password comparison example we used previously, we could make the server sleep for a random amount of time before returning an answer.
At a first glance, if the timing variation in the comparison is of a few microseconds, then sleeping around a second or so would seem to completely mask this signal.
Unfortunately, this doesn’t work.
The problem is that we can filter out the noise through statistical analysis. Let’s say that we have our timing variation $t$, which is constant (given a fixed guess), and then our random sleep time $X$. The total wait time becomes a random variable:
$$ t + X $$
If we take the average, we get:
$$ t + E[X] $$
since $t$ is a constant. Now, if we simply subtract away $E[X]$, we get:
$$ t $$
which is our signal!
Of course, we can’t actually observe the average. What we can do, on the other hand, is take many samples, and use those to estimate what the expected value is. Using that information, we can filter out the noise that’s been artificially created, and recover the timing signal.
Because of this, adding in timing noise can only act as a mitigation, and not a particularly effective one at that.
Blinding operations
Roughly speaking, blinding is a technique where instead of computing a function $f$ directly on some input $x$, you first encode the input differently, in a way that can still be decoded after applying the function. The idea is that while the function $f$ may not be constant-time, it will leak information about the encoded version of $x$, but not $x$ itself.
One example of this is in RSA. Instead of encrypting a message as $m^e$, you can instead generate a random nonce, and encrypt a masked message $(mr)^e$. Exponentiation, unless implemented correctly, leaks a lot of information about its input. By using blinding, we hide the input, mitigating this source of information.
These aren’t perfect mitigations, for several reasons. One of these is that the encoding process itself might leak information through timing side-channels. Regardless, this remains a popular mitigation for RSA.
Timing leaks in Go
Go has a big number library as part of its standard library. While this library has all the operations you might want, and is quite performant, as far as I can tell. Unfortunately, its operations are filled with timing leaks: [3].
This is fine, since this API is intended to be a general-purpose Big Number library.
Unfortunately, this library is used for Cryptography not only
outside of Go, but even inside its own standard library. For example, Go’s RSA
implementation uses math/big. It does use blinding, so the most obvious
timing attacks are mitigated, but there’s likely plenty of vulnerability remaining.
The timing leaks in math/big come from a two principal sources:
variable-time algorithms, and its representation of numbers.
Leaky algorithms
The arithmetic operations in math/big are intended for general-purpose
use, and concentrate on being performant, without regard for
timing leaks. Because of this, many operations take variable execution
paths depending on their input. For example, exponentiation
might conditionally perform a multiplication, based on the bits of
another number. This kind of conditional choice is present
throughout the library, and is a source of timing leaks.
Unpadded numbers
Because Big Numbers are dynamically sized, operations can’t help but leak information about the size of their inputs. Unfortunately, Go makes sure that the size of a number is tightly bound to its actual value, by removing any unnecessary zeros. For example, if you were working with numbers modulo $1000$, you might want to always use 3 digits, representing $9$ as:
$$ 009 $$
Go would instead remove this extra padding:
$$ 9 $$
This means that subsequent operations would leak how small this value is, and we might be able to distinguish it from larger values. While seemingly innocuous, this kind of padding information can actually lead to attacks [4].
What does constant-time mean?
So, we’ve seen what the problem is, but how far can we go in actually solving it? If Big Numbers are dynamically sized, how can we possibly make our operations constant-time? What would constant-time even mean in this context?
The key here is to understand that by constant-time, we don’t mean that operations can’t take a varying amount of time. Instead, we mean that the timing signal generated by our operations doesn’t leak any secret information.
True vs announced length
Big Numbers are indeed dynamically sized. Operations using these numbers will leak how much space our numbers are taking up.
This seems like a problem at first, until you realize that we can lie about how big our numbers actually are. Our CPU registers are 64 bits long. A number like $3$ only takes 2 bits, but the circuitry doesn’t take less time to process $3$ compared to $18446744073709551615$ just because more of the bits are set in the latter.
Similarly, we can work with numbers that are padded to be a certain length, without revealing this padding at all.
It becomes important to distinguish the announced length of a number, from its true length. The announced length is the space used by a number, including padding, and will be leaked in operations using that number. The true length is the minimal number of limbs needed to represent a number, and should not be leaked.
For example, if we’re working modulo a public $N$, which is ~ 2048 bits long, we only need 2048 bits worth of limbs. We can make sure that all of our values use up that space completely. Our operations will leak that our numbers are 2048 bits long, but everybody already knows this! If we have a small number, like $3$, which doesn’t need all that space, we make sure to not leak the fact that its upper limbs are all $0$.
Our numbers will be dynamically sized, but should only be sized according to publicly known information, such as a public modulus, or a protocol driven bitsize.
Better algorithms
We also need to make sure that our operations don’t leak any information about the values composing our numbers. This entails (among other consequences) that we can’t look at the bits of a number to conditionally execute some piece of code, since this would leak information about the number’s actual value.
Essentially, every operation involving our Big Numbers needs to be either amended, or rethought completely, to make sure that our logic only leaks timing information based on public information, such as the announced length of our inputs.
Leaking modulus sizes
For Cryptography, modular arithmetic is a very common mode of operation. When working modulo $N$, you only need values up to $N - 1$, so this dictates the size of the numbers you’ll be working with. Because of this, it’s desirable to make sure that $N$ itself has no superfluous padding: your operations have fewer limbs to process, improving performance.
Furthermore, many algorithms like to make the asssumption that $N$ has no padding. Some operations (e.g. modular reduction) would like to use the most significant bits of $N$, which ends up leaking the exact bit length of $N$.
Thankfully, this assumption seems to be mostly fine in the common usages of modular arithmetic in Cryptography.
Usually, your modulus is going to be either a fixed parameter of the protocol, or part of the public key (like in RSA). In that case, it’s obviously fine to leak its length.
On the other hand, there are some points where the modulus should be kept secret. For example, to generate an RSA key, you have your modulus $N = pq$, the product of two primes, and you need to invert $e$ modulo $(p - 1)(q - 1)$. Leaking this value would be bad: learning the factorization of $N$ would allow an adversary to recover your private key. On the other hand, it’s mathematically clear that this value is roughly the same length as $N$, so leaking its bitsize isn’t actually detrimental.
Because of this assumption, it’s convenient to truncate the modulus, removing unnecessary padding.
Some basic techniques
So, that’s an overview of what we’re trying to achieve. Since this is just an introductory post, I won’t be going into the details of how exactly to accomplish all of this. I can, however, give a little taster for the kinds of contortions you have to do.
Some rules of thumb
Timing attacks can be quite subtle, but I have a working model of how to avoid them, which is quite pessimistic, but also simple:
- Loops leak the number of executions
for i := 0; i < N; i++ {
}
This will leak the value of N.
- Conditional statements leak which branch was taken, no matter what
Code like:
if condition {
foo()
} else {
bar()
}
will leak the whether or not condition was true or false, regardless
of what code is in either branch.
- Accessing memory leaks the index / address accessed
If I do:
array[secret]
this leaks the value of secret.
These are just a few “rules of thumb”, but already severely constrain the kind of code you have to write. You also need to be careful that the code you write doesn’t accidentally get optimized to suddenly violate these rules either.
Handling choices
So, if you can’t have a conditional statement based on some secret value, how do you handle choice? Many algorithms will need to do something different based on the numbers they’re working with.
Fundamentally, the idea is to do both options, and then to select between them in a constant time way. Instead of having your condition as a boolean, you could have it as a bitmask, either:
0b1111..
or
0b0000..
depending on the result of the condition.
You can then select between two numbers, through bitwise operations:
func Mux(mask, a, b Word) Word {
return (mask & a) | (^mask & b)
}
If the mask is all 1s, you select the first input, otherwise, you end up selecting the second input. So, instead of doing something like:
var x Word
if condition {
x = foo()
} else {
x = bar()
}
you’d instead perform both operations, and then select the right one afterwards:
xFoo := foo()
xBar := bar()
x := Mux(condition, xFoo, xBar)
This doesn’t have a timing leak anymore, since you can’t observe whether or not
foo() or bar() was executed.
This is just a rough idea of how the basic building block works. You also need to build more complicated operations on type of this, allowing you to conditionally manipulate entire arrays of numbers, instead of just individual limbs.
Looping on announced lengths
Most operations involving big numbers will loop on the length of the numbers involved. For example, adding two numbers will pair up the limbs composing each input. We need to make sure that this announced length is indeed public information, since it gets leaked.
Furthermore, you also can’t really loop on other conditions. For example, you can’t make a loop like this:
for a != b {
doStuff(a, b)
}
Not only does the condition itself leak, which might not be good, but now the
number of steps taken depends on the values of a and b.
(A few operations are actually based on a loop like this.) In each case, you need
to amend things to take a rigid number of steps, based only on the announced
lengths of the inputs, perhaps doing “nothing” for a while.
Safenum
This brings us to the actual work. So far, we’ve written a library, in Go, providing an implementation of constant-time Big Numbers (see above for what we mean by “constant-time”).
All of the operations necessary for cryptography should be present, and there’s only a few hanging fruit left in terms of obvious performance improvements. Comparing against Go’s standard library, we’ve gotten performance down from 260x slower, all the way to only 4x slower (comparing exponentiation with a ~3000 bit modulus). This is actually relatively good, because constant-time exponentiation is theoretically 2x slower (without windowing), assuming multiplication is just as fast.
The basic API approach
The API provides a type representing arbitrary numbers in $\mathbb{N}$.
type Nat
Each number also carries around an implicit “announced length”, which should be public. The actual value of a number will not be leaked, but the announced length can be.
The announced length of a number is set implicitly based on the operations creating it.
For example, you have:
func (z *Nat) SetBytes([]byte) *Nat
This will set the length of z depending on the length of the slice of bytes.
Another example is addition, where you pass in the number of bits the output should have:
func (z *Nat) Add(a *Nat, b *Nat, capacity uint) *Nat
When doing modular arithmetic, the size of the modulus dictates the size of the output instead:
func (z *Nat) ModAdd(a *Nat, b *Nat, m *Modulus) *Nat
The Modulus type is similar to Nat, except that it’s allowed to leak its true length.
Why Go?
As mentioned a few times now, the main output of this project is a library written in Go. The reasons for choosing Go are mainly circumstantial, as opposed to fundamental technical reasons.
In a vacuum
If you were to choose a language for this project, without any concern over what the likely consumers of the project would be, I think Rust would likely be the best choice.
I think the reasons for this would be:
- Good performance
- Easy control over compiler output
- Portability
- Interoperability with other languages (via C FFI)
Go has the disadvantage of being less portable, and having a few more layers between you and the assembly output. Having control over this can be important, since the compiler might violate your assumptions about code organization with respect to timing leaks.
Some core operations in math/big are actually implemented in assembly,
amounting to a noticeable 50% boost in performance (on my machine).
In Rust, writing these core operations in many platform-specific assembly
files would likely not be necessary. Furthermore, it would be easier
for us to implement new core primitives, rather than being restricted to
the ones already implemented in math/big.
Being useful
With all that said, language choices for projects are not made in a vacuum. Arguably, the most important consideration is who the library is going to be used by. Most of the potential consumers inside of the DEDIS lab would like a Go API, which heavily skews things in that direction.
Furthermore, Go’s FFI isn’t ideal for a library of isolated routines like this. The problem is that there’s a lot of overhead when switching from Go code over to another language. Paying this overhead for each individual arithmetic operation in a larger crypto protocol would be too expensive.
This motivates the usage of a library written in Go itself.
Fitting in math/big
Another goal of the library is to be potentially upstreamable to Go itself,
eventually addressing [3]. Because of this, we make use
of the assembly routines already implemented in Go for math/big.
By designing the library with this in mind, we make potentially migrating the work
back into the standard library much easier later on.
Conclusion
Hopefully this was at least an interesting overview of the work I’m doing this semester, which I once again should mention is being done at EPFL’s DEDIS lab, under the supervision of Professor Bryan Ford, without whom I would be having substantially less fun right now 8^)
This post was initially intended to be rehashed version of a 7 minute intro talk I gave a couple weeks ago, but ended up being substantially longer. I think I’ll be making a more in-depth post soon enough, talking about some details on how operations work. This is also a talk I’ll need to be giving in a couple weeks. Once the code has solidified a bit more, I’d also like to provide a comprehensive post detailing every single algorithm we end up using. I don’t think there’s a complete resource out there yet, although BearSSL does have a nice page about this: [5]. Unfortunately, this doesn’t cover all the tricks you actually need.
References
[2] Page, D. "Theoretical Use of Cache Memory as a Cryptanalytic Side-Channel", 2002