This is a post going over the basic concept of defining objects through Universal Properties, in Category Theory, with explanations and examples in Haskell.

Universal Properties allow us to characterize objects not by their internal structure, or some kind of internal description, but in the unique way they relate to other things. This kind of description is powerful, because it shifts the focus from the content of each object, to how different objects relate to eachother. This is the focus of Category Theory more generally.

The Basics

The usual way of defining an object through a Universal Property goes something like this. You’re working in some category $\mathcal{C}$. You can characterize some universal object $U$ in terms of how it relates to other objects. Usually this means that you have a unique morphism into or out of $U$ making some kind of diagram commute.

You can think of this as saying that $U$ is the “best way” to solve some kind of problem.

I’m obviously being a bit vague here, but examples will follow shortly.

Initial

Let’s make this much more concrete. Our first universal object is that of an Initial Object. This object is characterized as follows:

An object $X$ is initial in $\mathcal{C}$ precisely when there exists a unique morphism $U \to A$ for every other object $A$ in $\mathcal{C}$.

We have some kind of diagram like this:

for any choice of $A$.

With $\bold{Set}$

Now, let’s make things even more concrete, and pick a specific category: $\bold{Set}$. This is the category with sets as objects, and normal functions as morphisms.

Does this category have an initial object?

Yes! $\emptyset$ is in fact the initial object. This is because we can define a function $\emptyset \to A$ for any other object $A$. A function $B \to C$ is really an assignment of a one element of $C$ for each element of $B$. If you pick $c \in C$ for each element $b \in B$, then you have a function. Since the empty set has no elements, we don’t have any choices to make, so we’re done!

In Haskell

There’s a “category” $\bold{Hask}$ of Haskell types and functions. You can basically take this category as being equivalent to $\bold{Set}$. Naturally, the “empty type” is going to be initial in $\bold{Hask}$:

data Void

This is the empty type, since there’s no way to construct it. How do we create a map to any other type?

absurd :: Void -> a
absurd _ = let a = a in a

Now, we cheat here by creating an infinite loop, but notice that it’s not actually possible to end up in the infinite loop. To do so, you’d have to produce a value of type Void, which is impossible!

Terminal

The dual notion to an initial object is a terminal object. Instead of having a unique map from our object. we have a unique map to our object:

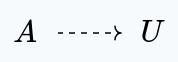
In $\bold{Set}$, this object is the set with a single element: $\bullet := \{\bullet\}$.

Given some other set $A$, we define our unique map $f$ as:

$$ f(a) = \bullet $$

In Haskell

This translates straightforwardly to Haskell. Here, the type with a single element is (). Our universal map is defined in a similar way:

f :: a -> ()
f _ = ()

Uniqueness

Can there be more than one initial or terminal object?

Yes, but that object must be isomorphic to the initial / terminal object.

Let’s prove this for initial objects. Let’s say we have two objects $U, U'$ satisfying the initiality property.

We have unique maps $f : U \to U'$ and $f^{-1} : U \to U'$ between them. We can compose these to give us maps $f ; f^{-1} : U \to U$, and $f^{-1} ; f : U' \to U'$. But, the identity functions $1_U : U \to U$ and $1_{U'} : U' to U'$ are also maps. But, since any function out of $U$ or $U'$ must be unique, we have:

$$ \begin{aligned} f ; f^{-1} &= 1 \cr f^{-1} ; f &= 1 \cr \end{aligned} $$

which is precisely the condition for $f$ to be an isomorphism.

This can be summarized concisely by the following commutative diagram:

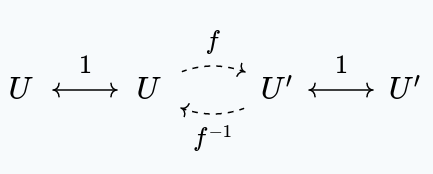
This proof can be reused almost piecemeal to show that terminal objects are unique up to isomorphism as well.

Universal Representation

The implication of this fact is that any representation of a type defined by a universal property is isomorphic.

For example, let’s take the terminal object (). We can represent this using the property itself!

data Terminal where
  Terminal :: forall a. a -> Terminal

Now, we’re using GADT syntax, because it makes this construction very clear. We have a function to convert an a into Terminal, given any type a. In practice, this is an existential type. Given an element of Terminal, we have some a, but we don’t know what type it actually had. It could have been anything.

Of course, since this encodes the universal property, it must be isomorphic to ():

iso1 :: Terminal -> ()
iso1 _ = ()

iso2 :: () -> Terminal
iso2 _ = Terminal ()

We can do the same trick for the initial object Void:

data Initial where
  Initial :: (forall a. a) -> Initial

We’d like to encode this as forall a. Initial -> a, but we have to settle for the less intuitive forall a. a. The idea is that given some instance of Initial, we have an element a, for any type of a.

As expected, we have an isomorphism:

iso1 :: Initial -> Void
iso1 (Initial v) = v

iso2 :: Void -> Initial
iso2 v = Initial (absurd v)

Products

The familiar product (a, b) is also characterized by a universal property! Notably, for any other type Z with projectors Z -> a, and Z -> b, there’s a unique morphism Z -> (a, b) making the following commute:

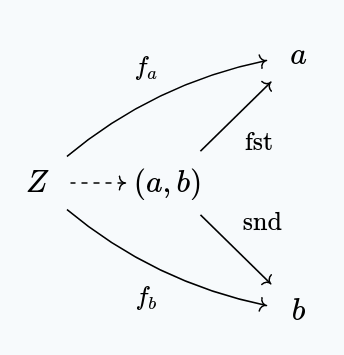
One way of thinking about this is that (a, b) is the simplest way of making a type that can project onto both a, and b. We have no extra information whatsoever. If we did have some extra information, say:

data User a b = User
  { name :: String,
    a :: a,
    b :: b
  }

We could always just pluck out the projections:

pluck (User _ a b) = (a, b)

We can define our “universal product” directly with the same technique’s we’ve seen earlier:

data Product a b where
  Product :: forall z. (z -> a) -> (z -> b) -> z -> Product a b

For any type z, if you have a projector to a and b, then you have a function z -> Product a b, by the universal property.

This is isomorphic to the standard product (a, b):

iso1 :: Product a b -> (a, b)
iso1 (Product fst' snd' z) = (fst' z, snd' z)

iso2 :: (a, b) -> Product a b
iso2 tuple = Product fst snd tuple

Sums

We can also encode the sum Either a b using a similar universal property. The definining characteristic of Either a b is that we can construct it from an a, or a b alone. Now, there might be other types that we can make with an a or a b, but Either a b is the simplest one.

Formally, for any other type z, with a constructor a -> z and b -> z, you have a function Either a b -> z, making the following diagram commute:

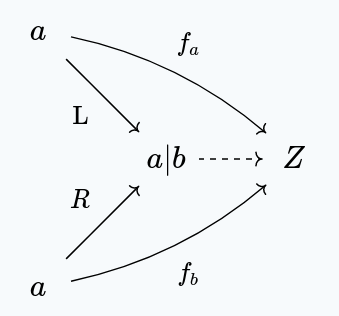
The intuition is the Either a b is the smallest type in which we can embed both elements of a and b. There might be larger types in which this embedding is possible, but we can always go through Either a b to make this embedding happen.

Using our standard trick, we can encode Either a b as a universal property

data CoProduct a b where
  CoProduct :: (forall z. (a -> z) -> (b -> z) -> z) -> CoProduct a b

In some sense, this type is the “opposite”, or dual to the Product we saw earlier, which is why it’s sometimes called the CoProduct.

Once again, it’s easy to show that an isomorphism exists:

iso1 :: CoProduct a b -> Either a b
iso1 (CoProduct f) = f Left Right 

iso2 :: Either a b -> CoProduct a b
iso2 (Left a) = CoProduct (\l _ -> l a)
iso2 (Right b) = CoProduct (\_ r -> r b)

Conclusion

This was just a quick post to go over the basics of objects defined using universal properties, along with some examples of encoding them in Haskell.

The main weakness of this approach is that we can’t capture properties that aren’t structural. For example, we have a functions $f : A \to W$, and $g : B \to W$, and we want to find the subset of the product $(A, B)$, such that $\pi_A : f = \pi_B : g$ (this is called the pullback), then our universal representation fails to capture this property, since this isn’t encoded structurally.

Anyways, there’s a lot more to explore, but I wanted to get some of the basics out there in a quick post.