This is the second post in the Haskell in Haskell series.

In this post, we’ll go over creating a lexer for our subset of Haskell. This stage of the compiler goes from the raw characters in our a source file, to a more structured stream of tokens.

We’ll finally be digging into some serious code this time, so get your editor ready if you’re following along!

The full code for this part is available here, for reference.

1 mile overview

Before we go dive into the code, let’s first get an idea of what this part is about. What job is the lexing phase trying to accomplish? What is it responsible for? What kind of output will we produce?

Making Tokens

The first goal of the lexer is to take our raw source code, a blob of characters (String, in Haskell), and figure out how to group these characters to make the Parser’s job easier.

As a reminder, the Parser is going to take our tokens, and then produce a complete representation of the source code. The Parser could work directly on characters, but this would be more complicated. We would be worrying about character level concerns, at the same time as higher level structure. Having a separate lexing phase gives us a nice separation of concerns here.

The Parser will need to use context to do its job. For example, when parsing an expression, it knows not to try and read out things related to types. On the other hand, the lexer (at least the part that spits out tokens) can be made to work without context.

The lexer just reads in characters, and spits out tokens. After spitting out a token, the lexer is in the exact same “state” that it started with. The lexer has minimal knowledge about context.

What tokens?

So far we’ve talked about “tokens”, or “clusters”. A good analogy is that our source code is like a sentence in English: the sentence is composed of raw characters, ditto for source code. The words in the sentence make up the tokens in our source code. And finally, the parse tree gives us the meaning of the sentence, or the source code.

So, we want to split up our source code into the tokens that compose it. What kind of tokens will we end up using?

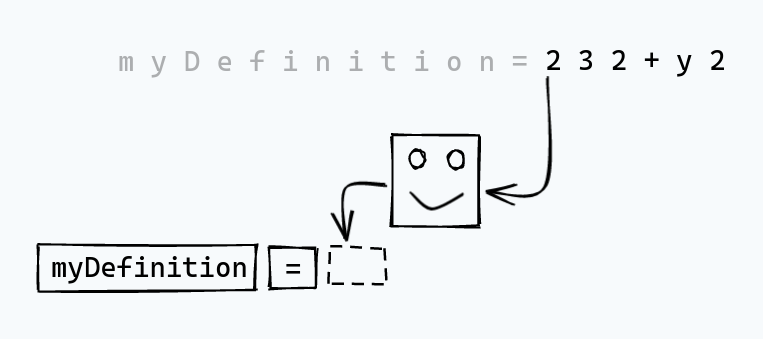
As an example, consider this simple definition:

myDefinition = 232 + y2

In terms of raw characters, we have:

m y D e f i n i t i o n  =  2 3 2  +  y  2

In terms of tokens, we’d like to end up with:

Here, we’ve first separated out an identifier, that must be taken as a whole. It makes no sense to process myDefinition as anything but a single unit in the parser. We also have two operators, =, and +. We also have a literal, 232. It doesn’t make sense to treat a literal as anything but a unit.

We’ll be going over the details of what tokens we’d like to define, and how exactly we’re going to go about lexing them out of our source code later. But keep this idea in mind: we’re trying to separate out our source code into little units, all to make our Parser much simpler.

Generating Whitespace

Our lexer will also have a job much more specific to Haskell. Haskell has one critical feature that makes parsing it a bit tricky: whitespace.

We’re quite used to the whitespace sensitivity as Haskell programmers. Most programming languages nowadays don’t even require semicolons, even if they do still use braces for layout. On the other hand, most people don’t know how Haskell actually uses braces and semicolons out of the hood.

For example

let { x = 2; y = 3 } in x + y

Is a perfectly valid expression. However, most people would write this as:

let x = 2
    y = 3
in x + y

and they may not even be aware that you could use the braces and semicolons instead. In fact, not only is the braced version an option, but the whitespaced version is nothing more than syntax sugar for this way of doing things.

When Haskell sees:

let x = 2
    y = 3
in x + y

It understands that you really mean:

let {
  x = 2;
  y = 3
}
in x + y

and infers those pesky braces and semicolons accordingly.

In fact, when you have multiple definitions at the top level, like:

x = 2
y = 3
z = 4

This is also lingo for a braced version:

{
x = 2;
y = 3;
z = 4
}

What we’re going to be doing is adding an extra mini-stage that looks at the whitespace in our program, and inserts the correct semicolons and braces to reflect the meaning of the indentation.

We could do this as part of the parser, but this would make the parser much more complicated than it otherwise needs to be. Doing this as an extra step between the more traditional lexer and the parser makes things much cleaner, and much more maintainable.

If you don’t understand exactly what constructs end up using indentation to insert braces and semicolons, that’s normal: I haven’t explained it yet :). We’ll be going over this whole business in much more detail when we implement this system, so that it’s fresh in our heads.

Our First Stage

So, having seen what we’re going to be accomplishing in this part, let’s actually start the scaffolding for what we want to do.

A trivial Lexer

The first thing we want to do is to create a trivial lexer. This will serve as a stubholder for now. Our goal here is to write the command line wrapper around this code first, and then expand it to make an actual lexer later.

Anyhow, we need a Lexer module, so let’s add that to our exposed-modules in our .cabal file:

library
  ...
  exposed-modules: Ourlude
                 , Lexer
  ...

And then, let’s create a file for this module, in src/Lexer.hs:

{-# LANGUAGE LambdaCase #-}
{-# LANGUAGE TupleSections #-}
module Lexer (Token(..), lexer) where

import Ourlude

We’re using two extensions here to add some extra features to the code in this module.

The first LambdaCase, allows us to replace expressions like:

\x -> case x of
  Foo -> ...
  Bar -> ...

with:

\case
  Foo -> ...
  Bar -> ...

which explains the naming of this feature.

The second, TupleSections allows us to use partially apply tuples, in the same way you can do operators. For example, you can do:

map (,3) ["A", "B"]
[("A", 3), ("B", 3)]

Without the extension, you’d have to write the less terse: \x -> (x, 3) instead.

Both of these extensions are included in this module because they simplify some code here and there. LambdaCase, in particular, will even be used pretty heavily throughout the project.

We also have import Ourlude, in order to import the custom prelude we defined last time.

For now, let’s create a “stub” implementation of our lexer:

data LexerError = UnimplementedError deriving (Eq, Show)

data Token = NoTokensYet deriving (Eq, Show)

lexer :: String -> Either LexerError [Token]
lexer _ = Left UnimplementedError

These are the types that our lexer will eventually end up producing. Given a string, containing the source code we need to lex, we should either produce an error, of type LexerError, or the list of tokens we managed to lex.

Right now, we just have a dummy token type, and an error indicating that our lexer has not been implemented yet.

Making a CLI program

Before we actually implement these functions, we’re first going to integrate the lexer into our command line program, so that the user can run it on an actual file. We can reuse this boilerplate for the other stages of our compiler as well. With this out of the way now, we can focus on the guts of the compiler as we move forward.

First, let’s add the imports we’ll be needing in Main.hs:

import Control.Monad ((>=>))
import Data.Char (toLower)
import qualified Lexer
import Ourlude
import System.Environment (getArgs)
import System.Exit (exitFailure)
import Text.Pretty.Simple (pPrint, pPrintString)

We import our Lexer module, since we’ll be using that here. We also import our prelude, of course, as well as some small helpers like >=>, and toLower. We have some IO stuff we’ll be using like getArgs :: IO [String] for getting the arguments passed to our program, as well as exitFailure :: IO (), to quit the program if an error happens.

pPrint and pPrintString come from the library we mentioned last time , which can format any given string in a nice way.

Stages: The Idea

We’re going to make a bit an abstraction over the concept of a stage. Our compiler will be composed of various stages, such as the lexer, the parser, etc. Each stage takes in some input, and produces some output, potentially failing with an error. Our lexer takes in a String as input, produces [Token] as output, and fails with LexerError. Our stage abstraction should represent this concept of input, output, and errors.

We also want to be able to produce some kind of function, or IO procedure to execute, knowing up to which stage we want to proceed. So if the user does haskell-in-haskell lex foo.hs, we know that they want to stop and see the output of the lexing stage, whereas haskell-in-haskell type foo.hs would mean stopping after the type-checking phase, etc. We need to use our stage abstraction to construct some kind of IO action, and figure out which of these actions to run based on this first argument. So if we see lex, we run lexAction, if we see type we run typeAction, etc.

Stages: The Implementation

The first thing we need is some kind of opaque error type. We want this so that our stage abstraction doesn’t have to keep track of the error type, for one, and also so that we can annotate the errors produced by that stage with some metadata, like the name of that stage.

So, in Main.hs, let’s create:

data StagedError = StagedError String String

Unfortunately, the two arguments are easily confused, but the first will be the name of the stage, and the second will be the error produced by a given stage, already converted to a String.

We want to be able to transform Either ThisStageError ThisStageInput to use this error convention, so let’s create:

stageEither :: Show e => String -> Either e a -> Either StagedError a
stageEither name m = case m of
  Left e -> Left (StagedError name (show e))
  Right a -> Right a

Given a name (which is presumably that of a given stage), we can massage the error into a StagedError by showing the error, and putting the name beside it.

We want to be able to print this StagedError type in a nice way, so let’s create:

printStagedError :: StagedError -> IO ()
printStagedError (StagedError name err) = do
  putStr name
  putStrLn " Error:"
  pPrintString err

This uses pPrintString from the pretty-simple library to print out the error in a nice way.

With this error type in hand, we can create our stage abstraction:

data Stage i o = Stage
  { name :: String,
    runStage :: i -> Either StagedError o
  }

So, Stage is parameterized over an input type i, and an output type o. We use this to create a function taking input i, and producing output o, potentially failing with a StagedError. We also have the name of the stage as an extra bit of metadata.

We might have Stage String [Token] for our Lexer, Stage [Token] SyntaxTree for our Parser, etc.

Our lexer is of the form String -> Either LexerError [Token]. If we squint at this a bit, we see i -> Either e o. We want to transform these kinds of function into Stage, so let’s create a little helper:

makeStage :: Show e => String -> (i -> Either e o) -> Stage i o
makeStage name r = Stage name (r >>> stageEither name)

We can work on any function i -> Either e o, so long as it has an error we can use show with, as explained earlier. We also include the name of the stage here.

We can go ahead and define a stage for our lexer:

lexerStage :: Stage String [Lexer.Token]
lexerStage = makeStage "Lexer" Lexer.lexer

Everything works out nicely, because we took care to design our little Stage abstraction around how the different parts of our compiler actually work.

We’d also like to be able to compose our stages together; that’s why we’re creating this whole abstraction. Let’s make a little helper operator:

(>->) :: Stage a b -> Stage b c -> Stage a c
(>->) (Stage _ r1) (Stage n2 r2) = Stage n2 (r1 >=> r2)

See the similarity here with:

(>>>) :: (a -> b) -> (b -> c) -> (a -> c)

One detail we do here is that the name of the composed stage is just the name of the second stage. We could’ve opted to make a new name, like Lexer >-> Parser or something. This option actually makes more sense, because each stage depends on the previous one, and we never run one half of the stages without the other half. We only stop early, sometimes.

Now, let’s add some code to create an IO action from a given Stage:

printStage :: Show b => Stage a b -> a -> IO ()
printStage (Stage name r) a = case r a of
  Left err -> do
    printStagedError err
    exitFailure
  Right b -> do
    putStrLn (name ++ ":")
    pPrint b

The idea is that we create a function accepting the Stage’s input, and then printing out whatever output it produces, or printing the error, and terminating the program with exitFailure, indicating that a failure occurred.

Parsing Arguments

We’re getting close to having a little program we can run! The next thing we’ll be doing is defining a type for the arguments our program accepts from the command line:

data Args = Args FilePath (String -> IO ())

The first part will be path to the Haskell code we’re handling, but the second part is a bit unorthodox. The idea is that it represents the stage we’ve parsed. We could have created an enum for which stage the user wants to go up to, and then interpreted that to make an IO action, but it’s easier to just parse out an action directly. The reason we have this String -> IO () representation is that every single stage is able to hide behind it. We’ll be creating Stage String b for each of our “go up to this part” stages. They all take in the source code as input, but the output varies. We can use printStage to get around this, and store all of the stages in the same way.

Here’s how we’ll be reading the stages:

readStage :: String -> Maybe (String -> IO ())
readStage "lex" = lexerStage |> printStage |> Just
readStage _ = Nothing

For now, we just accept a single stage “lex”, which runs the only stage we have, and prints out the results.

Then, to use the args we’ve produced, we just read in the source file, and then run the action:

process :: Args -> IO ()
process (Args path stage) = do
  content <- readFile path
  stage content

Since we’ve already read in the stage as String -> IO (), this works out just fine.

We can now write a function to parse out all of the arguments:

parseArgs :: [String] -> Maybe Args
parseArgs (stageName : file : _) =
  Args file <$> readStage (map toLower stageName)
parseArgs _ = Nothing

This takes in the list of arguments as passed in to the program, and returns the parsed arguments. The only trick here is that we lower case the stage name, so that “lex”, “LEX”, “lEx”, etc. refer to the same stage. For example for:

haskell-in-haskell lex file.hs

We would have:

["lex", "file.hs"]

as our arguments.

Remaining Glue

Finally, we can modify main to glue all of these functions together:

main :: IO ()
main = do
  stringArgs <- getArgs
  case parseArgs stringArgs of
    Nothing -> putStrLn "Unrecognized arguments"
    Just args -> process args

getArgs :: IO [String] returns the command line arguments passed to us. We then use these to parse out Args, printing out a failure message, or proceeding with the process function we defined earlier.

Now we can actually run the lexer, to see something like

> cabal run haskell-in-haskell -- lex foo.hs
Lexer Error:
UnimplementedError

Oof, that was a mouthful, but now all of this boilerplate is out of our way for the rest of the compiler. Adding new stages is going to be a breeze!

How do you make a Lexer?

That was a dive into some practical Haskell, although mostly boilerplate. Now let’s go back up a layer of abstraction, and think a bit about what a lexer really is, and how it works in theory.

At the end of the day, our lexer will be scanning over our input string character by character, outputting tokens as it goes.

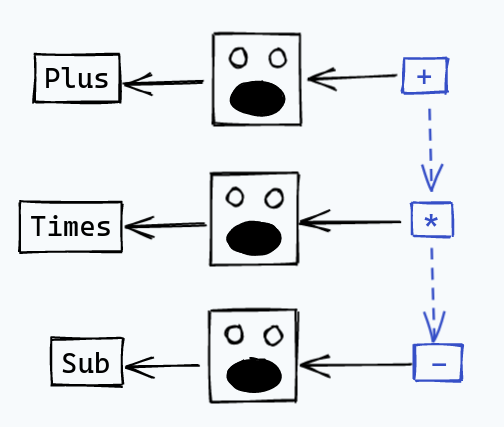
For simple operators, it’s easy to understand how our lexer is going to work. For example, if we have some operators like:

+*-

the lexer can see the +, and then immediately spit out a Plus token, or something like that. When it sees the *, it spits out Times, with -, we get Sub, etc.

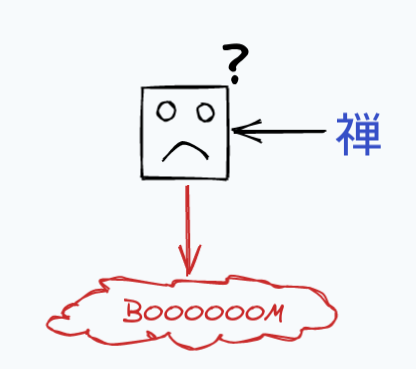
If our lexer sees a character it doesn’t know, it can blow up with an error:

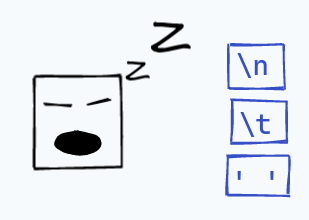
For some other characters, the lexer will simply ignore them:

If we only need to lex out single characters, then an interesting thing to notice is that our lexer keeps track of no state whatsoever. After seeing a single character, the lexer is straight back to the same state it started with, ready to accept another character.

Character Classes

Our lexer will have to produce tokens composed of more than just a single character of input. Integers, for example. We want to accept things like 3, 234, 2239034. Integer literals can be arbitrary strings of digits. To handle this, our lexer needs to enter a different “mode”, or “state” as soon as it sees a digit. Instead of immediately producing some output, it instead shifts to a mode where it tries to consume the digits that remain, and only “breaks out” once it sees something that isn’t a digit. At that point, it can produce the token for that integer literal, and return back to its initial state.

Many more of the tokens we produce will involve multiple characters. For example, to match out against a string literal like "Hello World", we need to realize that a string literal is happening when we see Athe ", and then keep on consuming characters for that literal until we see the closing ".

Quite a few tokens in our language will be keywords. For example, let, where, data, type. These can be consumed using “modes” or “states” as well. For example, when we see an l, our lexer could enter a mode expecting to see e, followed by t to finish out the keyword.

So far we’re developing a vision of a lexer as a “finite state machine”. The idea is that at any point in time, our lexer is in a given state, and we can move to different states as we see different characters, potentially spitting out some tokens along the way. For example, a state machine that accepts arithmetic tokens like 2 + 23 * 44 would look like:

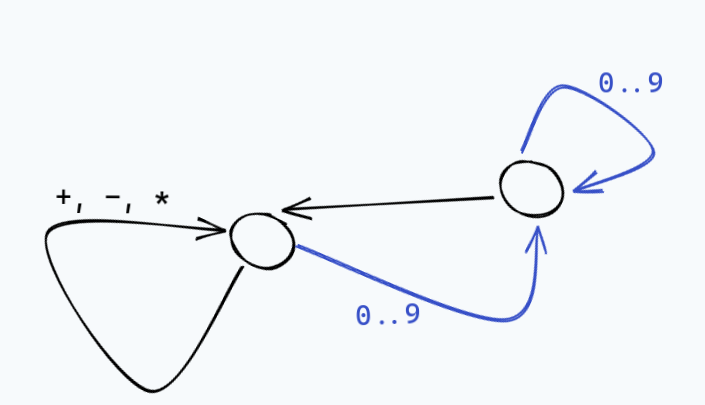
This state machine idea is also intimately connected to regular expressions, and in fact all the different classes of characters that make up our tokens correspond to regular expressions, and we should be able to recognize whether or not our source code is lexically valid with a giant regex.

There’s a rich theory around the connection between lexers, regular expressions, and state machines, so I’ll refer you to other resources if you’re interested in that.

There’s a great chapter on lexing in Crafting Interpreters, which explains these concerns in much more detail.

Engineering a Compiler also has a good section on lexing, if you really want a lot more detail.

Longest Match

Another issue we’ve completely glossed over is that of conflicts between different classes of characters. We’ve specifically looked at nice examples where everything is in a completely different bubble, with no interaction between the different characters.

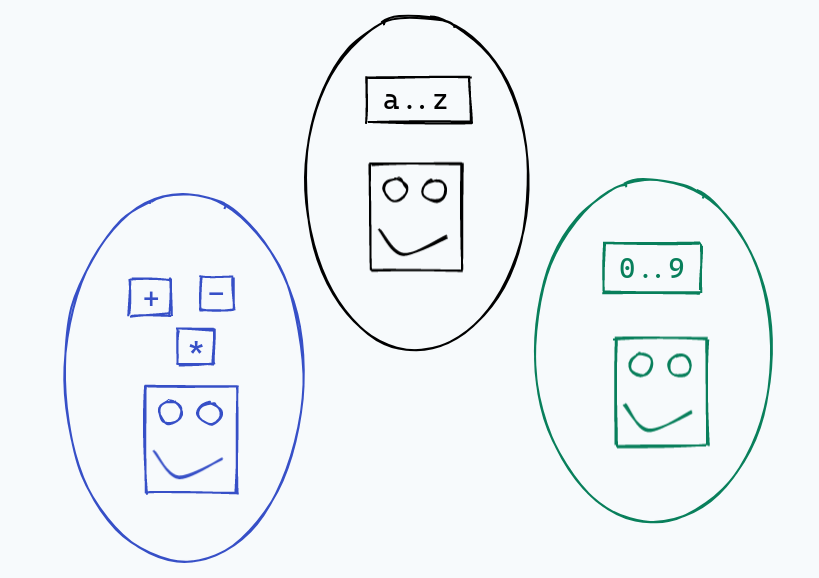
Now, the biggest source of ambiguity is between identifiers and keywords. For example, if we see where, then that is the keyword where. No ambiguity whatsoever, but if we add just one character, to get where2, then suddenly that’s an identifier, and where2 = 3 is a valid bit of Haskell. So our previous idea of seeing a w, and jumping straight towards assuming we’ve seen the start of the keyword where is not going to work. In fact, if we have some kind of rule like: “an identifier is a lower case alpha character followed by any number of alphas and digits”, then it conflicts with every single keyword!

How do we choose which to pick?

The idea is that we should keep applying a rule greedily. That is, if there are two possible ways of pulling out a token from some string, we pick out the one that consumes more input. So if we see wherefoo, we can parse this in two ways:

where (Keyword) foo
wherefoo (Identifier)

But we should clearly accept the second one, because it consumed more of the input. This rule is enough to disambiguate keywords and identifiers, as long as we give priority to keywords, for when we have an exact match.

Lexer Combinators

So, that was a quick overview of some of the abstract ideas around lexing, and now let’s dive into creating a little framework in Haskell for building up our lexer. The idea is that we want to be able to build up a large lexer for Haskell source code from lexers for smaller parts.

To do this we’ll use Lexer Combinators, a topic I’ve already talked about previously. See that post if you want even more detail and explanation after what we see here.

The Basic Definition

The basic idea of a Lexer Combinator is that a lexer is nothing more than a function taking in some input, in our case, a String, and then either throwing an error, because it does not recognize what it sees, or consuming part of the input, returning a value, along with the remaining part of the input it hasn’t touched.

So, something like String -> Either LexerError (a, String) in Haskell syntax. In fact, let’s go ahead and go back to src/Lexer.hs.

Imports

As is going to become a custom throughout this series, we’re add all of the imports we need for the rest of this module right away:

import Control.Applicative (Alternative (..), liftA2)
import Control.Monad.Except (ExceptT, MonadError (throwError), runExceptT)
import Control.Monad.State (State, gets, modify', runState)
import Data.Char (isAlphaNum, isDigit, isLower, isSpace, isUpper)
import Data.List (foldl', foldl1')
import Data.Maybe (listToMaybe, maybeToList)
import Ourlude

We have some utilities for checking properties of characters, some convenient list folds that sadly aren’t in the default Prelude, and the helper listToMaybe. The other monadic stuff will be introduced in due time as we get to using these utilities

Errors

Let’s go ahead and redefine the type of errors that our lexer will be producing:

data LexerError
  = Unexpected Char
  | UnexpectedEOF
  | UnmatchedLayout
  deriving ()

The first, Unexpected char, is used when we encounter a character that we don’t know how to handle. UnexpectedEOF is when we reach the end of the input string before we’re done lexing some token. For example, if you start a string literal, but never end it, like "abbbbb, then you’ll get an UnexpectedEOF when all of the input has been consumed.

The last error is related to whitespace inference, and will be explained more once we reach that part.

We can go ahead create a utility function to throw the right error given the remaining input:

unexpected :: String -> LexerError
unexpected [] = UnexpectedEOF
unexpected (c : _) = Unexpected c

If there’s no input left, and we’re in an unexpected situation, then we weren’t expecting the input to end so early, and should produce an UnexpectedEOF error, otherwise seeing whatever character is at the front of our input was the problem

The Core Type

Now let’s define the actual data type for lexers:

newtype Lexer a = Lexer {
  runLexer :: String -> Either LexerError (a, String)
}

So a Lexer is nothing more than a wrapper around a function taking in some input, and either failing with a LexerError, or producing a value of type a, and the remaining string that we have yet to consume.

We can go ahead and write a few basic “building blocks” that we’ll be needing later.

The first lexer we’ll make is one that accepts a single character matching a predicate, producing whatever character was accepted:

satisfies :: (Char -> Bool) -> Lexer Char
satisfies p =
  Lexer <| \case
    c : cs | p c -> Right (c, cs)
    rest -> Left (unexpected rest)

This inspects the input we’ve been given, and only consumes the first character if it can pull it out of the string, and it satisfies the predicate we’ve been given.

An immediate application of this lexer is:

char :: Char -> Lexer Char
char target = satisfies (== target)

which will match an exact character. So we might do char '+', for example.

Now we need to implement some fundamental typeclasses for Lexer, which will be used for composing them together.

Functor

The first is the venerable Functor class:

instance Functor Lexer where
  fmap f (Lexer l) = Lexer (l >>> fmap (first f))

Here we have

fmap :: (a -> b) -> Lexer a -> Lexer b

as the concrete type for this function. All this does really is do some plumbing to change the output our lexer produces; fmap has no effect whatsoever on what characters a lexer accepts.

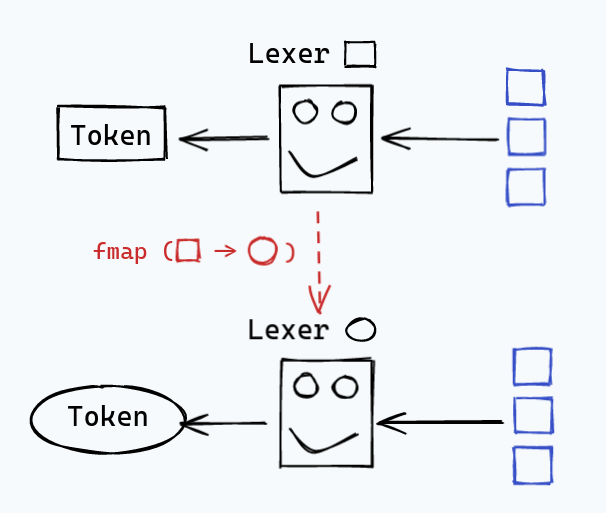
This also gives us access to other functions that use Functor, for example, we could now transform fmap (const Plus) (char '+') into Plus <$ char '+', since <$ :: Functor f => a -> f b -> f a is defined for any type implementing Functor.

Applicative

The next type class is Applicative, which in concrete terms, requires us to define two functions:

pure :: a -> Lexer a

(<*>) :: Lexer (a -> b) -> Lexer a -> Lexer b

The concrete idea here is that pure will create a Lexer that produces a value with consuming any input whatsoever. <*> will allow us to combine two lexers sequentially, using the function output by the first, and the value output by the second to produce a final result.

So, let’s implement it:

instance Applicative Lexer where
  pure a = Lexer (\input -> Right (a, input))
  Lexer lF <*> Lexer lA =
    Lexer <| \input -> do
      (f, rest) <- lF input
      (a, s) <- lA rest
      return (f a, s)

pure is pretty self-explanatory, we simply pass along the input without consuming anything, as explained before.

For <*>, things are a bit more interesting. Notice how we’re making use of do for Either LexerError here. Another important detail is the we use the remaining input of the first lexer to feed to the second lexer. This might seem like a bit of an arbitrary choice, but it’s actually important.

For example, (,) <$> char 'A' <*> char 'B' should accept the string "AB". To do this, we need to have consumed the character A before “moving on” to the second lexer.

In fact, now that we have Applicative, we can get a lexer recognizing an entire string “for free”

string :: String -> Lexer String
string = traverse char

This uses the very cool traverse :: Applicative f => (a -> f b) -> [a] -> f [b], which in our case, first makes a bunch of lexers recognizing each respective character in a given string, and then sequences them to recognize the entire string, one character at a time.

Alternative

We can create somewhat sophisticated lexers parsing long strings by chaining them sequentially with <*>, but one thing that’s sorely missing is the ability to choose between different options. I can take two lexers and say “I want to lex A, followed by B”, but I can’t say “I want to lex A, or B”. Our tokens are going to need this mechanism. Each token is going to be one of the options we can choose from.

Thankfully, there’s a type class for this: Alternative. Concretely, it requires us to implement:

empty :: Lexer a

(<|>) :: Lexer a -> Lexer a -> Lexer a

<|> implements the intuitive notion of choice we want, and empty acts as the identity for this operation, that is to say:

empty <|> lexerA = lexerA = lexerA <|> empty

Now, <|> is going to have to run both of the parsers. If one of them fails, then we have to rely on the result of the other one. If both succeed, then we have to implement the longest match rule we talked about earlier. If this results in a tie, then we want to give priority to the left one.

Let’s implement the class:

instance Alternative Lexer where
  empty = Lexer (Left <<< unexpected)
  Lexer lA <|> Lexer lB =
    Lexer <| \input -> case (lA input, lB input) of
      (res, Left _) -> res
      (Left _, res) -> res
      (a@(Right (_, restA)), b@(Right (_, restB))) ->
        if length restA <= length restB then a else b

For empty, we have a lexer that will fail on any input.

For <|>, we pattern match on both the results given the same input, at the same time. If one of them fails, we rely on the other result. If both succeed, we need to dive in a bit more, and compare the lengths of the remaining inputs. We pick the result that has less input remaining, i.e. that has consumed more input, i.e. that is the longest match. On ties, when the remaining inputs have equal length, we still choose a. This means that we’re biased towards the left lexer, as we talked about earlier.

We can once again put this to use, and create a helper letting us create a lexer choosing one out of many options:

oneOf :: Alternative f => [f a] -> f a
oneOf = foldl1' (<|>)

This will work with other Alternative types, and not just Lexer, although we won’t be exercising that option here.

With that done, we now have all of the building blocks and combinators we need to make a real lexer for Haskell!

Implementing the Lexer

Alright, we’ve created a bit of a framework for building lexers. This might seem a bit abstract right now, but will all fit into place very quickly as we put it into practice.

Tokens

The first thing we need to do is actually define the type of tokens we want our lexer to return.

We need a couple classes of tokens, basically:

1. Keywords, like where, let, case
2. Operators, like +, ->, ::
3. Literals, which we have for Bool, Int, and String
4. Hardcoded primitive types, in our case Bool, Int, and String
5. Identifiers, which come in two flavors in Haskell.

I apologize for the information dump, but it’s easier to just write them all out, since most of them are just dumb labels:

data Token
  = Let -- `let`
  | Where -- `where`
  | In -- `in`
  | Data -- `data`
  | Type -- `type`
  | If -- `if`
  | Then -- `then`
  | Else -- `else`
  | Case -- `case`
  | Of -- `of`
  | Underscore -- `_`
  | OpenParens -- `(`
  | CloseParens -- `)`
  | OpenBrace -- `{`
  | CloseBrace -- `}`
  | Semicolon -- `;`
  | DoubleColon -- `::`
  | ThinArrow -- `->`
  | VBar -- `|`
  | BSlash -- `\`
  | FSlash -- `/`
  | Plus -- `+`
  | PlusPlus -- `++`
  | Dash -- `-`
  | Asterisk -- `*`
  | Equal -- `=`
  | Dollar -- `$`
  | LeftAngle -- `<`
  | Dot -- `.`
  | LeftAngleEqual -- `<=`
  | RightAngle -- `>`
  | RightAngleEqual -- `>=`
  | EqualEqual -- `==`
  | FSlashEqual -- `/=`
  | VBarVBar -- `||`
  | AmpersandAmpersand -- `&&`
  -- An Int literal
  | IntLit Int -- An Int literal
  -- A String literal
  | StringLit String
  -- A Bool literal
  | BoolLit Bool
  -- The type `Int`
  | IntTypeName
  -- The type `String`
  | StringTypeName
  -- The type `Bool`
  | BoolTypeName
  -- A name starting with an uppercase letter
  | UpperName String
  -- A name starting witha lowercase letter
  | LowerName String
  deriving (Eq, Show)

The literals for Int, String, and Bool have values of the corresponding types, as we might expect. Haskell has this peculiarity where identifiers come in two flavors, the upper case identifiers, like Foo230 and Baz240, which are used to indicate types, and lower case, like fooA343, or bazB334.

A lexer for tokens

Now, we can write a Lexer that produces these tokens!

We have:

token :: Lexer (Token, String)
token = keyword <|> operator <|> literal <|> name
  where
    with :: Functor f => b -> f a -> f (b, a)
    with b = fmap (b,)

    ...

with is nothing more than a little helper we’ll be using shortly. Our lexer is defined in terms of a handful of sub-lexers we’ll also be defining in that where block. The high-level idea is that we’re saying that a token is either a keyword, an operator, a literal, or a name. Notice that we put keyword to the left of name, so that keywords have priority over identifiers!

Keywords are defined as lexers accepting exactly the right string:

    keyword :: Lexer (Token, String)
    keyword =
      oneOf
        [ Let `with` string "let",
          Where `with` string "where",
          In `with` string "in",
          Data `with` string "data",
          Type `with` string "type",
          If `with` string "if",
          Then `with` string "then",
          Else `with` string "else",
          Case `with` string "case",
          Of `with` string "of",
          Underscore `with` string "_"
        ]

Here we’re using with in infix notation, in order to include the string along with the token, which we’ll be needing later. Another fun detail is that we consider _ to be a keyword. Whether or not something is a keyword is more so about making the parser’s job easier, rather than reflecting the semantics of the language. We could’ve made _ just a normal identifier, but then we would have had to do extra work to separate out this token in the parser.

Anyhow, let’s look at operators:

    operator :: Lexer (Token, String)
    operator =
      oneOf
        [ OpenParens `with` string "(",
          CloseParens `with` string ")",
          OpenBrace `with` string "{",
          CloseBrace `with` string "}",
          Semicolon `with` string ";",
          DoubleColon `with` string "::",
          ThinArrow `with` string "->",
          VBar `with` string "|",
          BSlash `with` string "\\",
          FSlash `with` string "/",
          Plus `with` string "+",
          PlusPlus `with` string "++",
          Dash `with` string "-",
          Asterisk `with` string "*",
          Equal `with` string "=",
          Dot `with` string ".",
          Dollar `with` string "$",
          LeftAngle `with` string "<",
          LeftAngleEqual `with` string "<=",
          RightAngle `with` string ">",
          RightAngleEqual `with` string ">=",
          FSlashEqual `with` string "/=",
          EqualEqual `with` string "==",
          VBarVBar `with` string "||",
          AmpersandAmpersand `with` string "&&"
        ]

Once again, we’re just mapping strings to labels. All of the code to do the lexing work is taken care of by the framework we set up before!

Now let’s move on to something a bit more interesting: literals:

    literal :: Lexer (Token, String)
    literal = intLit <|> stringLit <|> boolLit
      where
        ...

So, a literal is either an integer literal, a string literal, or a bool literal, as we went over above.

For integers, we have:

        intLit :: Lexer (Token, String)
        intLit =
          some (satisfies isDigit)
            |> fmap (\x -> (IntLit (read x), x))

So, some accepts one or more of a given lexer. It’s actually defined for any Alternative! We accept one or more digits, and then use read to parse that string of digits as an actual Int

For strings, we have:

        stringLit :: Lexer (Token, String)
        stringLit =
          char '"' *> many (satisfies (/= '"')) <* char '"'
            |> fmap (\x -> (StringLit x, x))

The idea is that we require a ", followed by many characters that are not the closing ", and then that closing ". Our manipulation with *> and <* just makes sure that we don’t include the delimiters in our string literal.

And finally, we have boolean literals:

        boolLit :: Lexer (Token, String)
        boolLit =
          (BoolLit True `with` string "True")
            <|> (BoolLit False `with` string "False")

This approach is the same we used for keywords and operators before, and makes sense since we only have two values for Bool.

Now the only remaining “sub-lexer” is for names, where we’ll also be including the names of primitive types:

    name :: Lexer (Token, String)
    name = primName <|> upperName <|> lowerName
      where
        ...

A name is either the name for a primitive type (with priority), a name starting with an upper case alpha, or a name starting with lower case alpha.

For primitive names, we use the same approach as with keywords:

        primName :: Lexer (Token, String)
        primName =
          (IntTypeName `with` string "Int")
            <|> (StringTypeName `with` string "String")
            <|> (BoolTypeName `with` string "Bool")

For normal names, we want a few helpers as well:

        continuesName :: Lexer Char
        continuesName = satisfies isAlphaNum <|> char '\''

        followedBy :: Lexer Char -> Lexer Char -> Lexer String
        followedBy l1 l2 = liftA2 (:) l1 (many l2)

        upperName :: Lexer (Token, String)
        upperName =
          (satisfies isUpper `followedBy` continuesName)
            |> fmap (\x -> (UpperName x, x))

        lowerName :: Lexer (Token, String)
        lowerName =
          (satisfies isLower `followedBy` continuesName)
            |> fmap (\x -> (LowerName x, x))

continuesName is a class of characters that can appear after the first character of an identifier, allowing us to “continue” that identifier. This includes any alphanumeric character, as well as the ', which Haskell also allows.

We then have a helper, followedBy, which parses the first class of things, followed by zero or more occurrences of the second thing. many, is like some, except it allows zero occurrences as well.

With these in hand, are two different kinds of name are simple to define. the difference is that one starts with an upper case character, and the other starts with a lower case character.

An actual lexer

Now, let’s actually replace our lexer function to use this framework:

lexer :: String -> Either LexError [Token]
lexer = runLexer (some token)

instead of token, which only parses a single token, we use some to parse one or more occurrences of a token. At this point, we should be able to lex out some interesting things, although we won’t be handling whitespace between tokens until then.

Let’s try out a few examples.

You can actually run these at this point, creating a file foo.hs to contain the examples, and then using:

cabal run haskell-in-haskell -- lex foo.hs

And then running this on:

x=2+2

should output

[ LowerName "x"
, Equal
, IntLit 2
, Plus
, IntLit 2
]

We can also accept things that make no sense syntactically:

x->::Int

which outputs:

[ LowerName "x"
, ThinArrow
, DoubleColon
, IntTypeName
]

We can already have a lot of fun doing things like this right now! It’s satisfying to start to see a bit of vim from our compiler. But we really need to be able to handle spaces, and also infer semicolons and braces!

Handling Whitespace

Right now we have a lexer for all of the basic building blocks of Haskell, but it can’t handle any whitespace at all! There are two aspects of whitespace that we’re going to be tackling in this section.

Haskell, like basically every language, allows you to put plenty of space between tokens. For example, what we can now lex:

x=2+2*2

could also be written in the prettier form:

x = 2 + 2 * 2

or even:

x   = 2    +    *    2

These should all generate the same tokens. The bits of whitespace contribute nothing, and should be ignored.

In C, for example, everything is delimited using braces and semicolons, so arbitrary amounts of both vertical and horizontal whitespaces are simply completely ignored when lexing. You could remove all whitespace from your program and get the same result.

In Haskell, on the other hand, whitespace can be significant, when it’s used to create layouts where braces and semicolons should be inferred. This layout inference is the second aspect that we’ll be working on, and is much more complicated than simply ignoring whitespace. In fact, because of this aspect, we can’t just take the easy approach of filtering out whitespace characters as a whole, and instead need to be quite picky about what whitespace we see, since vertical whitespaces acts differently than horizonal whitespace.

Haskell’s layout structure

I’m assuming that you’ve programmed a reasonable amount in Haskell before, so you’re probably familiar on an intuitive level with how you can use whitespace to layout blocks. In fact, you probably haven’t used braces and semicolons in your programs, and maybe you didn’t even know they were an option. Let’s try to go from our intuition about how things should work, to a more robust understanding.

As an example, consider something like:

x = foo + bar
  where
    foo = 3
    bar = 4
    
y = 3

The first rule that you’ve likely internalized is that everything at the same level of indentation continues whatever the current block is. Because foo and bar are at the same level of indentation, we expect them to be in the same block.

Similarly, x and y are in the same block. This rule also makes it so that we have to indent the where, so that it belongs to x, and is not seen as continuing the same layout that x and y belong to.

We also require that foo and bar are further indented than the where.

With explicit braces and semicolons, we have:

{
x = foo + bar
  where {
    foo = 3;
    bar = 4
  }
;
  
y = 3
}

This is just the realization of our implicit intuition about where scopes should be, and how they work.

A final rule we’ve all internalized is that layouts only happen after certain keywords.

When we see:

x =
  2 + 3
  * f x

everything after the = is just a single expression, all bound to x. This all belong to x because they’re further indented, but no layout has been introduced after the =.

If we generate semicolons like this:

x = {
  2 + 3;
  * f x
}

that would obviously not be correct.

on the other hand, from a lexical point of view, if we had:

x = a
  where
    2 + 3
    * f x

then we should insert a layout, and end up with:

{
x = a
  where {
   2 + 3;
   * f x
  }
}

The where keyword make us ready to see this kind of whitespace sensitive layout of code. The other keywords like this (for our subset) include let, and of.

Position Information

With our intuitive understanding, we’ve realized that it’s very important to keep track of “where” a token is, both “vertically”, and “horizontally”.

For example:

x = y

does not yield the same layout as:

x =

y

and

let
  x = 1
  y = 2 
in

should not yield the same layout as:

let
  x = 1
    y = 2
in

What column a token appears at is quite important. Whether or not a token is at the start of a line also matters. We’ll need to annotate our tokens with this position information.

So, in Lexer.hs, let’s create some types to represent this information:

data LinePosition = Start | Middle deriving (Eq, Show)

data Positioned a = Positioned a LinePosition Int deriving (Eq, Show)

Positioned a adds position information to something of type a. We include the a itself, followed by its LinePosition, and the exact column at which it appears.

What we’ll be doing soon enough is making a function [Positioned Token] -> [Token], using that extra position information to infer the necessary braces and semicolons.

Right now though, we just have [Token], without any position information, and no braces and semicolons.

Raw Tokens

In fact, our lexer simply blows up if it encounters any whitespace tokens, and we can’t handle comments either. The next order of business is being able to lex whitespace and comments along with normal tokens.

If we weren’t whitespace sensitive, we’d still need to do this. We would simply collect all of these tokens, and then filter them out from the final output. This way, we could allow arbitrary spacing between tokens, as well as comments in the source code, without affecting the rest of the tokens.

For our purposes, it’s important to keep these tokens, so we can annotate the other “normal” tokens with position information. We’ll be using the whitespace and comment tokens around them to figure out how they’re positioned within the file.

So, let’s define a new token type that adds these extra variants:

data RawToken
  = Blankspace String
  | Comment String
  | Newline
  | NormalToken Token String

Blankspace represents “horizontal” whitespace, i.e whitespace containing no newlines. For newlines, we have the Newline token. We also have comments, with the Comment constructor, and then finally a little wrapper for normal tokens, along with their string contents.

Let’s go ahead and create a lexer for these raw tokens:

-- A Lexer for raw tokens
rawLexer :: Lexer [RawToken]
rawLexer = some (whitespace <|> comment <|> rawToken)
  where
    rawToken = fmap (uncurry NormalToken) token
    ...

So, our raw lexer parses at least one occurrence of a raw token, which is either whitespace, a comment, or a normal token.

For comments, we need to parse a --, and then the rest of the line:

    comment = Comment <$> (string "--" *> many (satisfies (/= '\n')))

To allow for empty comments, we pick many instead of some.

Now, for whitespace, we can either have horizontal whitespace, or a single newline:

    whitespace = blankspace <|> newline

If we have multiple newlines, we’ll end up generating multiple tokens.

Horizontal whitespace is just one or more whitespace characters that are not newlines:

    blankspace =
      Blankspace <$>
        some (satisfies (\x -> isSpace x && x /= '\n'))

And a newline is generated when we see a \n:

    newline = Newline <$ char '\n'

With that, we can now parse out the whitespaces and comments. We could now make a lexer for “whitespace insensitive Haskell”, if we wanted to. We would replace some token with rawLexer, in our lexer function, and then filter out the normal tokens.

Positioning Tokens

The next step is using all of this information to annotate the normal tokens using the Positioned type we defined earlier. We want to have a function [RawToken] -> [Positioned Token]. Given the list of raw tokens, we produce a list of tokens with positions. In the process, all of the whitespace and comment tokens are discarded.

The basic idea of the algorithm is going to be a somewhat imperative one. We’ll keep track of (LinePosition, Int), which will serve as the position of the next token, when we end up producing it. As we see raw tokens, we’ll update this state, or actually produce a token positioned with this information.

In practice, we have this:

type PosState = (LinePosition, Int)

position :: [RawToken] -> [Positioned Token]
position = foldl' go ((Start, 0), []) >>> snd >>> reverse
  where
    go :: (PosState, [Positioned Token]) -> RawToken -> (PosState, [Positioned Token])

So, we’re folding from the left, and the accumulator will hold the current position information, as well as a list of tokens we’re producing. After the fold is done, we discard this position state, but keep the tokens we produced. We produce a new token by adding it the front of the list, so we want to reverse this order after we’re finished.

Before we define go, we need a little helper function eat:

eat :: PosState -> RawToken -> (PosState, Maybe (Positioned Token))

eat will take in the current position information, and a raw token, and then adjust the current position. It may also produce a token with position information, when we come across an actual token, and not one of the extra whitespace or comment tokens.

The implementation looks like this:

    eat :: PosState -> RawToken -> (PosState, Maybe (Positioned Token))
    eat (pos, col) = \case
      Newline -> ((Start, 0), Nothing)
      Comment _ -> ((Start, 0), Nothing)
      Blankspace s -> ((pos, col + length s), Nothing)
      NormalToken t s ->
        let token = Positioned t pos col
        in ((Middle, col + length s), Just token)

When we see a newline, regardless of what position we had earlier, the new position will be at the first column, at the start of the next line.

A comment acts in the same way, since a comment is effectively like a new line, in terms of positioning.

When we see blank space, we advance the current column, while keeping but our position at the start or middle of a line is left unchanged. If we were previously at the start of a line, and then see some blank space, we’re still at the start of the line, since we haven’t seen a “real” token yet.

When we see an actual token, we’re going to produce that token, along with the current position information. We then adjust the position information to now be in the middle of that line, and we move the column forward based on how long the string contents of that token were.

With that done, the implementation of go is straightforward:

    go :: (PosState, [Positioned Token]) -> RawToken -> (PosState, [Positioned Token])
    go (p, acc) raw =
      let (p', produced) = eat p raw
      in (p', maybeToList produced <> acc)

We adjust the position information according to eat, and add a token to our accumulator if eat happened to produce one.

Alrighty, now we have a little function to produce the position information for our tokens, all we need is to make an algorithm that uses all of this information to insert braces and semicolons in the right places!

A Stateful Algorithm

The algorithm we’re going to be working on is an imperative one. The idea is that we’ll be iterating over the positioned tokens, while keeping track of some bits of state, and then yielding tokens as we go. In response to the position information, we might modify our current state, or yield some extra semicolon or brace tokens. We also want to yield all of the original tokens from the source code.

Layouts

The first thing we need to keep track of are the layouts

data Layout = Explicit | Implicit Int

We distinguish between Explicit layouts, which are created by the user with {}, and Implicit layouts, which are inferred based on whitespace.

Let’s say we have some code like:

let {
  x = 3
} in x

When we see a {, we’ve entered an Explicit layout, and we need to keep track of this information, because we will not be inserting any semicolons while we remain in this layout, and we’ll also need an explicit closing brace.

On the other hand, if we have:

let
  x = 3
in x

then this is an Implicit layout, in fact Implicit 2, since the (zero-based) column where the layout is at is 2. This number matters, as we’ve seen before. This is because:

let
  x = 3
  y = 2
in x + y

has a very different meaning from

let
  x = 3
    y = 2
in x + y

The former should see a semicolon inserted between the two definitions, whereas the second will have us end up with x = 3 y = 2, as if they were on one line. Syntactically, this will get rejected by our parser, but our lexer isn’t going to bat an eye yet.

We also want to be able to nest layouts, like this:

let {
  x = let
    y = 3
  in y
} in x

To do this, we’ll be keeping a stack of layouts. This will allow us to push and pop layouts as we enter and exit them.

Expecting Layouts

Another rule we mentioned in passing before is that let, where and of are places where a layout can start. For example, when you have:

let
  x = 2
in x

After seeing let, we need to keep our eyes peeled for the next token, since that token might trigger the start of a new implicit layout. The column where that token is positioned becomes the column for that new layout as well.

On the other hand, if we see a { after a let, that indicates that we’re not going to be starting an implicit layout, in which case the indentation of that { doesn’t matter at all.

We’ll need to keep track of whether or not we’re expecting a layout. When we see let, where or of, we’ll set that to true, and then set it back once we’ve found the next token.

The Full State

The final thing we’ll need, mainly for convenience, is a way to yield tokens. Since we might want to yield extra tokens at certain points, it’d be nice to have a way to modify the state to have an extra few tokens in its “output buffer”. We’ll have a [Token], and then use : to add new items. Once we’ve traversed all of the positioned tokens, we can reverse this list, and return it, and this will become the final output for the lexer.

So, our full state looks like this:

data LayoutState = LayoutState
  { layouts :: [Layout],
    tokens :: [Token],
    expectingLayout :: Bool
  }

layouts is the stack of layouts we mentioned earlier, expectingLayout the flag for let, where, and of, and tokens is the “output buffer” we’ve just talked about. Our code will be inspecting this state, and modifying it, as it scans through the positioned tokens we feed it.

Contextual Computation

In this section, we have our first use of Monad Transformers to create a little context, or DSL, in which to do some kind of operation. We’ll be seeing plenty more of these throughout the rest of this series, so I think it’s a good idea to explain the general idea here. If you’re already familiar with some of the practical applications of Monad Transformers and the mtl library, then feel free to skim, or skip over this section.

In normal Haskell code, you’re just working with plain old values, and function application. When you add some definitions with let, say:

let x = f a b c
    y = g a b c
in x + y

There’s no code “in between” those two definitions. The order in which we defined things doesn’t matter. This is somewhat obvious, but consider a slightly different version of this code:

do
x <- f a b c
y <- g a b c
return (x + y)

This bit of code is quite similar to the first version, but something very important has changed: we’re now in a do block. Because we’re in such a block, it becomes important not only to consider each line, but also the order in which the lines occur, as well as what kind of Monad, or context the do block is for.

What do enables us to go from strictly pure computations, to computations in a given context, or augmented with some kind of extra capability. One of the contexts we used recently was Maybe. Maybe allows us to do some computation with the possibility of failure. do does the job of sequencing together all of the code, using the >>= function that Maybe implements. In the above example, if f were to return Nothing, then the result of the whole block would be Nothing.

There are other kinds of contexts that will be useful to us quite soon. One example would be State s. This allows us to have some computations that manipulate some state of type s. We can query for the current state, and also modify it. It’s as if we embedded a little imperative DSL into our Haskell code. Of course, State s is essentially sugar for s -> (a, s), and >>= does the drudge work of passing the correct state around as new states are returned. No mutation actually happens, but plenty of mutation is certainly expressed in the DSL provided by State s.

Where transformers come into play is in their ability to let us combine multiple contexts together. If we want the ability to fail with an error, and to manipulate a given state, we’ll need to combine both State s and Either e. This is where things like StateT and ExceptT are useful.

LayoutM

We can use these raw combinations directly, or encapsulate them behind a newtype. We’ll be using newtypes later on. The idea behind wrapping a stack of transformers behind a newtype is that the DSL we want to provide is quite different than that of the different transformers. The transformers are just an implementation detail for the little imperative language we want to embed.

In this case, we’ll be using a “naked” stack, but later on we’ll mostly be using newtype stacks.

We’ll be needing a context / stack for our algorithm, which we’ll aptly call, LayoutM:

type LayoutM a = ExceptT LexerError (State LayoutState) a

We’re combining two Monads here, Except LexerError, which allows to fail with errors of type LexerError, and State LayoutState, which allows us to inspect and manipulate the LayoutState type that we defined earlier.

We can go ahead and create a little helper that will run a computation in LayoutM, returning the tokens it produced, in the right order:

runLayoutM :: LayoutM a -> Either LexerError [Token]
runLayoutM =
  runExceptT >>> (`runState` LayoutState [] [] True) >>> \case
    (Left e, _) -> Left e
    (Right _, LayoutState _ ts _) -> Right (reverse ts)

The idea behind running the stack is that you need to unwrap the layers from outside to inside. So first we unwrap the ExceptT layer, and then unwrap the State layer. We need to provide a starting state, of course. That starting state indicates that no layouts have been seen yet, no tokens have been produced, but we are expecting a layout at the start of a file!

Finally, we’ll look at the output result, which will be (Either LexerError a, LayoutState), We don’t care about the output itself, only the tokens in the state, which we need to reverse, as explained before.

We expect a layout at the start of a file, because our source code will consist of multiple definitions:

x :: Int
x = y

y :: Int
y = 2

and we want to be able to infer the semicolons between the different statements, and thus the braces surrounding all of the code.

Basic Operations

As a bit of a warmup, let’s write a few of the fundamental operations we’ll be using. These make up a bit more of the “DSL” we’re making with LayoutM.

Yielding Tokens

The first operation we need is the ability to produce a token:

yieldToken :: Token -> LayoutM ()
yieldToken t = modify' (\s -> s {tokens = t : tokens s})

We modify the current state, producing a new state with the token at the front of our output buffer.

Layout Operations

We’ll be needing an operation to a push a new layout onto the stack:

pushLayout :: Layout -> LayoutM ()
pushLayout l = modify' (\s -> s {layouts = l : layouts s})

This one operates in the same way as yieldToken, except on layouts, instead of tokens.

And then we’ll need an operation to remove a layout from the stack:

popLayout :: LayoutM ()
popLayout = modify' (\s -> s {layouts = drop 1 (layouts s)})

We also want to be able to inspect the current layout:

currentLayout :: LayoutM (Maybe Layout)
currentLayout = gets layouts |> fmap listToMaybe

If layouts ends up being empty, then we’ll end up returning Nothing here.

An immediate application of this little helper is a function:

compareIndentation :: Int -> LayoutM Ordering

Which tells us whether or not an implicit layout starting at a given column would be considered less than (LT), equal to (EQ), or greater than (GT) than the current layout:

compareIndentation :: Int -> LayoutM Ordering
compareIndentation col =
  let cmp Nothing = GT
      cmp (Just Explicit) = GT
      cmp (Just (Implicit n)) = compare col n
   in fmap cmp currentLayout

The idea is that any implicit layout is greater than no layout at all, or an explicit layout. On the other hand, if we have another implicit layout, we need to compare the columns. We’ll be seeing how we use this comparison soon enough.

The Algorithm Itself

Alrighty, we’ve built in the background knowledge and some of the basic building blocks to actually start dissecting the layout algorithm itself. Here’s what it looks like:

layout :: [Positioned Token] -> Either LexerError [Token]
layout inputs =
  runLayoutM <| do
    mapM_ step inputs
    closeImplicitLayouts
  where
    ...

So layout takes in the positioned tokens we made earlier, and then converts them into a list of normal tokens, including the generated semicolons and braces. We might also fail with a LexerError.

What we do is run a layout action, which loops over the inputs using the step function, which will modify the state, and produce tokens, and then we have a function closeImplicitLayouts. The idea behind this operation is that at the end of a file, if any implicit layouts are still open, we need to generate the explicit closing braces for them.

For example, if we have something like:

x = y
  where
    y = z
      where
        z = 3

Then we want to end up with:

{
x = y where {
  y = z where {
    z = 3
  }
}
}

So we need to generate all of those closing braces when we reach the end of the token stream. Thankfully, since we keep a stack of the layouts we’ve entered, we’ll have 3 pending implicit layouts: one for the start of the file, and 2 others for the wheres.

So, we have the following definition:

    closeImplicitLayouts :: LayoutM ()
    closeImplicitLayouts =
      currentLayout >>= \case
        Nothing -> return ()
        Just Explicit -> throwError UnmatchedLayout
        Just (Implicit _) -> do
          yieldToken CloseBrace
          popLayout
          closeImplicitLayouts

We loop until there are no layouts left on the stack. If at any point, we see an explicit layout, then that’s an error. It means that we have something like:

{
x = 2

and we never close explicit braces ourselves. We have an unmatched { by the time we’re at the end of the file, and that’s an error.

Whenever we see an implicit layout, we generate the necessary closing }, and then remove that layout from the stack.

Another helper we’ll need is startsLayout:

    startsLayout :: Token -> Bool
    startsLayout = (`elem` [Let, Where, Of])

This encodes the fact we’ve talked about a few times, where let, where, and of are the tokens that start a layout.

The Step

The crux of the algorithm is the step function, which contains all of the core rules behind how layouts work in our subset of Haskell:

    step :: Positioned Token -> LayoutM ()
    step (Positioned t linePos col) = do
      expectingLayout' <- gets expectingLayout
      case t of
        CloseBrace -> closeExplicitLayout
        OpenBrace | expectingLayout' -> startExplicitLayout
        _
          | startsLayout t -> modify' (\s -> s {expectingLayout = True})
          | expectingLayout' -> startImplicitLayout col
          | linePos == Start -> continueImplicitLayout col
          | otherwise -> return ()
      yieldToken t

In certain situations, whether or not we’re expecting a layout matters, so we first retrieve that from the state.

Regardless of how we process that token, we will add it to the output buffer afterwards, hence the yieldToken t at the end of the case. We want to look at the token to decide what extra handling needs to be done though.

If we see }, that means that the user is intending to close a layout that they created explicitly using a {, and we handle that case in the closeExplicitLayout operation.

If we see a {, and we’re at a point in the stream where a layout can be started, because we’re after let, where or of, then we start an explicit layout, using startExplicitLayout.

Otherwise, the token itself doesn’t matter, but other properties and conditions do.

If that token starts a layout, then we need to set this flag to true in our state.

Otherwise, if we’re expecting a layout, then we should start an implicit layout at the column where this token appears.

So if we have:

let
  x =

After seeing let, we’re now expecting a layout. Then when we see x, we decide to start an implicit layout at column 2.

If we’re not expecting a layout, and we see the first token on a given line, then we’re continuing a layout that already exists, knowing that whatever layout we’re continuing is at the column col. This actually handles a few different cases, as we’ll see.

Closing Explicit Layouts

For closeExplicitLayout, the idea is that after seeing }, this must close an explicit layout started with {, and this layout must be at the top of the stack. The reason for this is that we don’t allow } to close implicit layouts itself.

For example:

{
let
  x = 2 }

this would be an error. This is because we start an implicit layout after the x, and } isn’t allowed to close that implicit layout itself.

Concretely, we have:

    closeExplicitLayout :: LayoutM ()
    closeExplicitLayout =
      currentLayout >>= \case
        Just Explicit -> popLayout
        _ -> throwError (Unexpected '}')

If the current layout is explicit, that’s what we expect, and we remove it from the stack, since the } has closed it. Otherwise, we throw an error, for the reasons mentioned above.

Starting Explicit Layouts

This is sort of the reverse operation. We need to push an explicit layout for the opening { we’ve just seen onto the stack. We also need to indicate that we’re no longer expecting a layout, since the { starts the layout we were expecting:

    startExplicitLayout :: LayoutM ()
    startExplicitLayout = do
      modify' (\s -> s {expectingLayout = False})
      pushLayout Explicit

Starting Implicit Layouts

For startImplicitLayout, let’s have a look at the code, and explain what’s going on with some examples afterwards. This function will be called when we’ve seen our first token (that isn’t a { or a }) after seeing a layout starting token.

    startImplicitLayout :: Int -> LayoutM ()
    startImplicitLayout col = do
      modify' (\s -> s {expectingLayout = False})
      compareIndentation col >>= \case
        GT -> do
          yieldToken OpenBrace
          pushLayout (Implicit col)
        _ -> do
          yieldToken OpenBrace
          yieldToken CloseBrace
          continueImplicitLayout col

Now, regardless of how we handle things, we’re no longer expecting a layout after this is over. We’ll have handled things, one way or another.

What happens next depends on how the column we saw this token at compares with the current indentation.

If we’re strictly further indented, then we start a new implicit layout, and push the { token that goes with it. Otherwise, we push a complete, but empty layout with a { and a matching } token, and then use continueImplicitLayout.

This catches the case where we have something like:

let
  x = 2 where
  y = 3
in x + y

After the where, we are indeed expecting a layout, and y at column 2 is the token we expect to handle that fact. But, since y = 3 is at the same level of indentation as x = 2, it belongs to the layout started after let! Because of this, this where block is actually empty, and the tokens we produce are:

let {
  x = 2 where {};
  y = 3
} in x + y

Now, if the y = 3 had been further indented:

let
  x = 2 where
    y = 3
in x

Then this would need to produce:

let
  x = 2 where { y = 3 }
in x

Continuing Implicit Layout

So continueImplicitLayout handles the case where we have some token at the start of a line, or after a layout token, that needs to continue the current implicit layout in some way. Another case we’ll handle here is closing that implicit layout automatically.

Layouts are closed when we see a token that’s less indented. For example:

x = y
  where
    y = 2

z = 3

The where layout closes when we see z = 3 indented less than y = 2, giving us:

{
x = y where { y = 2 };

z = 3
}

Concretely, we have:

    continueImplicitLayout :: Int -> LayoutM ()
    continueImplicitLayout col = do
      closeFurtherLayouts
      compareIndentation col >>= \case
        EQ -> yieldToken Semicolon
        _ -> return ()
      where
        closeFurtherLayouts =
          compareIndentation col >>= \case
            LT -> do
              yieldToken CloseBrace
              popLayout
              closeFurtherLayouts
            _ -> return ()

The first thing we do is close every implicit layout that we’re strictly below, for teh reasons we just went over. To close them we emit a }, and then pop the layout off of the stack.

Then we check whether or not there’s a layout matching our indentation exactly, in which case we need to emit a semicolon.

This is so that we have the semicolons in something like:

let
  x = 2
  y = 3
  z = 4
in x + y + z

With this way of doing things, we’ll be generating the semicolon necessary between the tokens when we see them continuing the layout, so we have something like:

let {
  x = 2
  ;y = 3
  ;z = 4
} in x + y + z

The rest of the logic we had earlier makes it so that by the time we call continueImplicitLayout, we know that there’s some other token before us, and we need a semicolon as a separator. That token will have use startImplicitLayout itself, producing the layout we find ourselves in.

Glue Code

We can now glue all of this together, and produce a lexer function that does all of these positioning rules:

lexer :: String -> Either LexerError [Token]
lexer input =
  runLexer rawLexer input >>= (fst >>> position >>> layout)

Some Examples

And that’s it! We’re done! We’ve made a complete lexer for our subset of Haskell, handling whitespace in all of its glory. For the sake of completeness, let’s see how it works in some examples.

As a reminder, we can run our lexer using:

cabal run haskell-in-haskell -- lex file.hs

First, if we just have some basic definitions:

x = 1

y = 2

z = 3

We see that the whole thing is surrounded in braces, and semicolons are inserted at the right spots:

[ OpenBrace
, LowerName "x"
, Equal
, IntLit 1
, Semicolon
, LowerName "y"
, Equal
, IntLit 2
, Semicolon
, LowerName "z"
, Equal
, IntLit 3
, CloseBrace
]

If we have a simple nested let:

z =
  let
    x = let
      y = 3
    in y
  in x

[ OpenBrace
, LowerName "z"
, Equal
, Let
, OpenBrace
, LowerName "x"
, Equal
, Let
, OpenBrace
, LowerName "y"
, Equal
, IntLit 3
, CloseBrace
, Semicolon
, In
, LowerName "y"
, CloseBrace
, In
, LowerName "x"
, CloseBrace
]

If you’ve followed along so far, congratulations, I hope that wasn’t too much typing! You can have quite a bit of fun trying out different programs, and seeing what output your lexer produces!

Conclusion

So, this post was longer than I expected it to be! Hopefully I did a decent job of introducing lexing, as well as the lexer for our subset of Haskell. I hope that the layout rules are much clearer now that you’ve actually had to implement all of their details. I’ve tried to organize the rules in a way that’s reasonably understandable.

As always, here’s. the full code for this part.

There’s a section in the Haskell ‘98 report that talks about Haskell syntax, and the layout rules, in particular. This might be an interesting read, and you can contrast the way they define rules there with the imperative algorithm we’ve set up here.

Crafting Interpreters is another fun and very approachable read if you want to know more about lexing.

In the next post, we’ll be going over parsing! By the end of that post, we’ll have gone from a simple stream of tokens to a full syntax tree for our subset of Haskell!