The usual definition of a Group excludes empty groups by definition. There are alternate definitions of a Group that allow us to include the empty set, and which are quivalent to the normal definition in all other cases.

This post explores this alternate definition, and the resulting differences with the normal concept of a Group.

What is a Group?

A Group is one of the most important structures in abstract algebra. Roughly speaking, Groups capture the notion of symmetry, or operations that can be undone.

Formally, a group consists of:

1. A set $G$
2. A function $\bullet : G \times G \to G$, called the group operation. We usually write this infix, as $g \bullet h$
3. A function $(-)^{-1} : G \times G$, called the inverse. We usually just write $g^{-1}$.
4. An element $e \in G$, called the identity.

Associativity

For all elements $a, b, c \in G$, we have:

$$a \bullet (b \bullet c) = (a \bullet b) \bullet c$$

This says that we can simply write $$a \bullet b \bullet c$$, and we can reduce things from left to right, or right to left, or anything in between, as long as relative order is observed. Very often we even omit writing out the operator, and denote $a \bullet b$ as $ab$. The operation in question is usually clear from the context.

Identity

For any element $a \in G$, we have:

$$ea = a = ae$$

So applying the identity element on the left, or on the right of $a$ has no effect. This is precisely why we call it the “identity”.

Inverse

For any element $a \in G$, we have:

$$a^{-1}a = e = aa^{-1}$$

So combining any element with its inverse, on either side, yields the identity in return.

The Trivial Group

As an important, albeit very simple, example of a group, consider the set ${e}$.

As hinted by how we named the element, we have no choice but to set our identity element to be $e$. There is no other element to choose from, after all.

We can then define: $e \bullet e = e$ and $e^{-1} = e$. Because there’s only one element, all of the group axioms will naturally hold.

The trivial group is pretty important because it relates to every other group in a natural way, as we’ll see later.

Other Non-Trivial Groups

The integers $\mathbb{Z}$ form a group under addition, in the natural way. The inverse of $x$ is $-x$. The identity is $0$, and addition $x + y$ forms our group operation. This group is a bit special, because it’s actually commutative, because $x + y = y + x$. This proeprty does not hold in every group.

If we take the integers modulo some number, say ${0, 1, 2, 3}$ for the integers modulo $4$, then this also forms a commutative group, in a similar way.

Individual groups aren’t the main concern of this post, so let’s move on to questions of emptiness.

The Empty Set

Before we can wonder whether or not there is an empty group, we should first look at the properties of the empty set.

The empty set $\emptyset$ or ${}$ has no elements. Because of this, every logical statement in the form:

$$\forall x \in \emptyset \ldots$$

is true. We say that a statement is vacuously true, in a case like this. One way of looking at this, is that there’s no way of disproving such a statement. You can’t possible provide a counterexample element in $\emptyset$, because there are no elements in $\emptyset$ to begin with.

Conversely, every statement of the form:

$$\exists x \in \emptyset \ldots$$

is false. This is because we’re not able to provide such an element $x$, precisely because there are no elements to begin with.

The Empty Group?

Going back to the standard definition of a group: $$(G, \bullet, (-)^{-1}, e)$$, we immediately hit a stumbling block.

There needs to be an element $e \in \emptyset$, but this is not possible, because $\emptyset$ contains no elements at all. So it seems that we can’t satisfy the properties of a group vacuously, because there are no elements that can serve as the identity.

So the identity poses a problem, but what about the other operations?

Vacuous functions

Although it might seem odd at first, we can in fact construct a function $\emptyset \to \emptyset$, from the empty set to itself.

Intuitively, if you manage to give me an element of the empty set, I can simply give it back to you. Thus, it’s possible to have a function $\emptyset \to \emptyset$

Formally, a function $f : X \to Y$ is defined (or can be defined) as a subset of the pairs $(X, Y)$. This kind of subset is sometimes called a relation. The subset has to satisfy the property:

$$\forall x \in X. \exists! y \in Y. (x, y) \in f$$

Or, in more familiar terms:

$$\forall x \in X. \exists! f(x) \in Y$$

This states the idea that a function is a unique assignment to a target value for each source value.

As we saw earlier, all statements of the form $\forall x \in \emptyset$ will be true. Thus we can define a function from the empty set to any other set, including itself.

THE Vacuous Function

Do these functions have any structure? It turns out not, they’re all the same. Any two functions $f, g : \emptyset \to X$ are equal.

To see why this is true, let’s look at how we define two functions to be equal in the first place.

Given $f, g : A \to B$ we say that $f = g \iff \forall a \in A. f(a) = g(a)$

So with $f, g : \emptyset \to X$, $f = g$ becomes $\forall a \in \emptyset. f(a) = g(a)$. But, this is vacuously true. Hence, any two functions going out from the empty set will be equal.

Another way of looking at this is that you can’t disprove equality. If I tell you that $f = g$, there’s no way to prove me wrong. You can’t give me any point, or element where they disagree, precisely because there are no elements to show me to begin with.

Vacuous Operations

Anyways, equipped with this knowledge, we can see that there exists a way to satisfy the two other group operations $\bullet : G \times G \to G$, and $(-)^{-1} : G \to G$, when $G$ is $\emptyset$. The problem comes solely from the postulate that there must be an element $e \in G$. If we could somehow do away with this property, then we’d be able to have empty groups.

But $e$ is in some sense determined by the connection with $(-)^{-1}$.

Because:

$\forall g \in G. gg^{-1} = e$

We can simply replace references to $e$ in our axioms of a group with references to $gg^{-1}$, for any element $g$.

Potentially Empty Groups

A (potentially) empty Group is a set $G$, along with two functions $\bullet : G \times G \to G$ and $(-)^{-1} : G \to G$ satisfying:

$$\forall a, b, c. \quad a \bullet (b \bullet c) = (a \bullet b) \bullet c$$

$$\forall g. \quad g^{-1}g = gg^{-1}$$

$$\forall g, h. \quad g^{-1}gh = hgg^{-1}$$

Thus, the empty set $\emptyset$ is a perfectly fine Group of this sort, because all the axioms are vacuously true, with both operations defined by the unique function $\emptyset \to \emptyset$.

Relation with Normal Groups

If we have a nonempty / standard Group $G$, then $gg^{-1} = e = g^{-1}g$, and the rest of the properties of potentially empty groups will follow.

If we have a potentially empty group, and we’re not working with the empty set, we can go in the other way. Even though it’s not explicit in the axioms, we can actually show that $gg^{-1} = hh^{-1}$. That is, there is only a single identity element. To see why this is the case, consider two different identity elements $e$ and $e'$. Then consider:

$$ge = ge'$$

$$g^{-1}ge = g^{-1}ge'$$

$$e = e'$$

So there’s a unique identity element. Thus we can pick out this element, and get back to the normal definition of a group.

If we’re working with an empty set, then we can’t pluck out this element.

Relation with the Trivial Group

What’s interesting is that the way you define the trival group is the same way that you define the empty group.

We have $\emptyset \times \emptyset = \emptyset$, as well as ${e} \times {e} = {e}$. Then there are unique functions ${e} \to {e}$ and $\emptyset \to \emptyset$. For both of these sets, there is a unique way of making them a Group. So really, looking just at the structure of the group itself, there’s no way to distinguish the two.

In the general context of functions, there’s no way to distinguish the empty set from the trivial set just by looking at functions involving that set. If I give you one of the two sets, and ask you to tell them apart just by looking at functions involving just that set, you cannot actually find a difference.

It’s only when looking at the connections from this set to the other sets that you find the difference. The difference is that the emptyset has a unique function to any other, and the trivial set has a unique function from any other set (we have no choice but to map every element to $e$).

So, there aren’t actually any new groups introduced by this concept, we have a new “synonym” of the trivial group. Internally, we can’t tell the two apart. But how do they connect to other Groups?

Group Homomorphism

To talk about how Groups are connected, we need to talk about Group Homomorphisms, structure preserving functions between Groups.

Formally, a Group Homomorphism $\varphi : G \to H$ between Groups $G, H$ is a set function $G \to H$, satisfying:

$$\forall g, h. \quad \varphi(gh) = \varphi(g)\varphi(h)$$

$$\forall g. \quad \varphi(g^{-1}) = \varphi(g)^{-1}$$

$$\varphi(e) = e$$

It is clear that the identity function $G \to G$, sending every element $g \in G$ to itself is a homomorphism.

Because of this, we can form a category, with objects nonempty Groups, and morphisms group homomorphisms. This category is usually denoted $\bold{Grp}$.

Potentially Empty Homomorphisms

What about homomorphisms between potentially empty groups? The only change in the definition is that we don’t necessarily have an identity element $e$, so we can remove that line. On the other hand, because we preserve inverses:

$$\varphi(gg^{-1}) = \varphi(g)\varphi(g)^{-1}$$

So identity elements are de facto preserved, just not explicitly.

This also forms a category, with the additional object for the empty Group. We shall denote this as $\bold{Gr}\emptyset\bold{up}$.

Different Categories?

How do these categories differ? Well, the only difference we’ve encountered so far are about the empty group. All of the morphisms that exist between nonempty groups also exist between potentially empty groups.

Initial and Terminal

One critical difference is that in $\bold{Grp}$, the trivial group ${e}$ is both initial and terminal.

The trivial set is trivial in terms of sets and functions, so it makes sense that it would be terminal here.

As far as initiality, there is a unique map ${e} \to G$ from the trivial group to any other group $G$. We map the single element of the group to the identity element always present in any other group. This condition is also demanded by the properties a group homomorphism must satisfy, so this morphism is unique.

Initially Empty

In $\bold{Gr}\emptyset\bold{up}$ however, there is no map ${e} \to \emptyset$, so the trivial group cannot be initial.

In fact, the empty group has stolen the initial property away from the trivial group. There is a unique set function from $\emptyset \to G$ to any other $G$. This function satisfies the properties of homomorphism, under our alternate set of rules, in a vacuous way.

New Morphisms?

Are there new morphisms ${e} \to G$ now that we’ve dropped the constraint $\varphi(e) = e$?

Consider $\varphi(e) := g$, for some element $g$. Then we need:

$$\varphi(e) = \varphi(ee)$$

$$g = gg$$

$$e = g$$

So, the only possible morphism is mapping to $e$. Hence, there are actually no new morphisms created, apart from the connections out of the empty group.

As a whole?

What do these categories look at as a whole?

$\bold{Grp}$

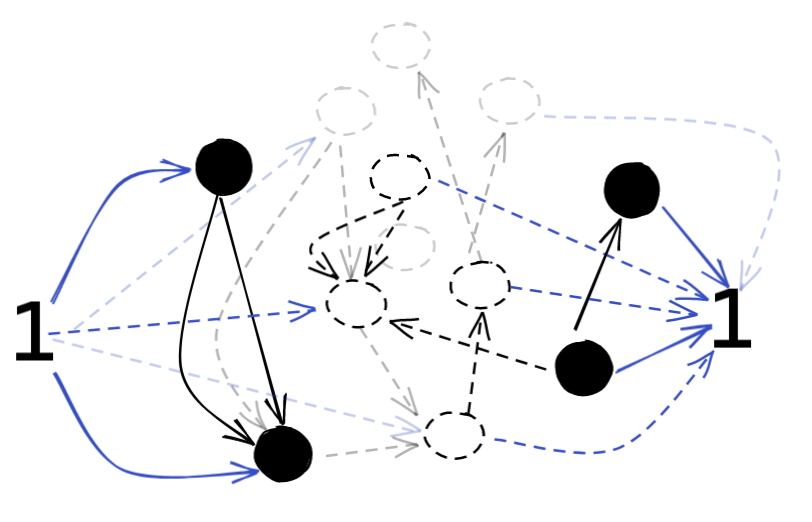
This is a rough sketch of what the category $\bold{Grp}$ looks like. We have a bunch of stuff in the middle, which isn’t too important. The trivial group $1$ serves as an initial and terminal cap, on both ends of the category. The blue arrows denote the unique morphisms involved.

$\bold{Gr}\emptyset\bold{up}$

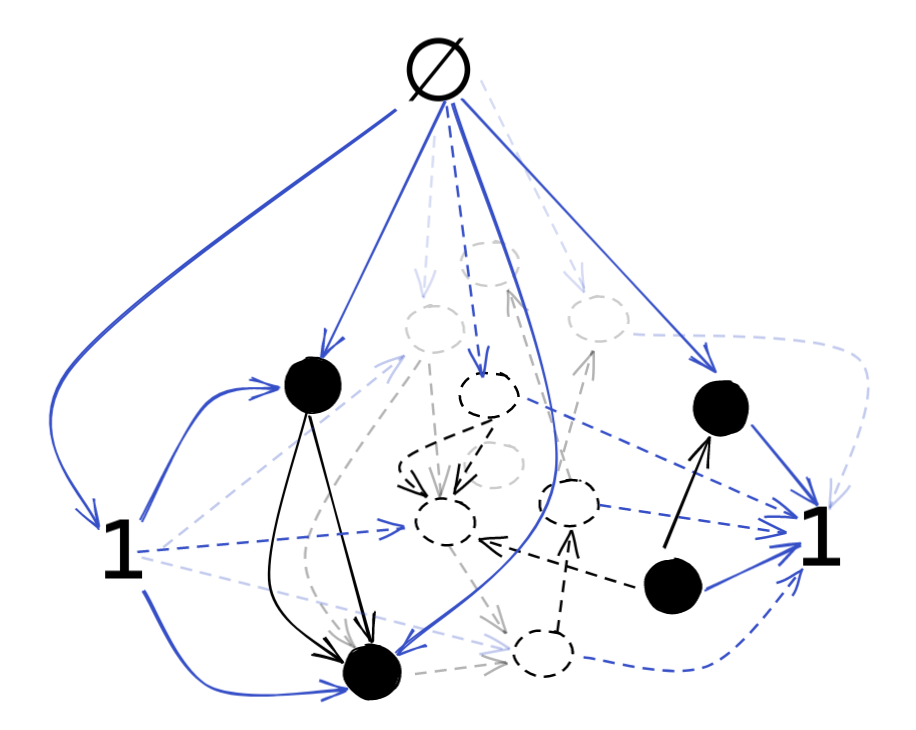
All of the standard groups are preserved completely. We just have a new initial group to replace the old one. The empty group $\emptyset$ sits above the old category, mapping down in unique morphisms.

Connecting Both Categories

Seeing both categories together, it’s easy to imagine oconnections, or functors between them.

A functor needs to map each group to another group, and each morphism to another morphism, in a way that preserves composition.

To get a functor $\bold{Grp} \to \bold{Gr}\emptyset\bold{up}$, we can simply fully embed everything underneath the empty group $\emptyset$.

For the other direction, we can map everything in a natural way, but what do we do with $\emptyset$?

Well, given its internal structure, it should probably map to ${e}$, that way we can preserve its initiality as well. The initial morphisms from $\emptyset$ will map down to initial morphisms from ${e}$.

So we have functors $L : \bold{Gr}\emptyset\bold{up} \to \bold{Grp}$ and $R : \bold{Group} \to \bold{Gr}\emptyset\bold{up}$, defined in a very natural way.

Isomorphic?

Do these connections show that the categories are isomorphic?

For that to be true, we’d need $R \circ L = 1$ and $L \circ R = 1$, where $1$ is the identity functor.

Well, $L \circ R$ is indeed the identity, because we first embed the entire category of $\bold{Grp}$, and then retreive it.

As for $R \circ L$, this does indeed work out, except for $\emptyset$, which ends up at ${e}$ after the round trip.

Because of this, the categories are not isomorphic. In fact, they’re not even equivalent, which would require the round trip to end up at an isomorphic object, and not just the same object. But ${e}$ is not isomorphic to $\emptyset$, because we can’t even map ${e} \to \emptyset$.

Adjoint Categories?

On the other hand, we can do $\emptyset \to {e}$, so we might want to consider the weaker, but still important, notion of an Adjunction.

To show that $L \dashv R$ is an adjunction, we need to show that there exists natural transformations:

$$\eta : 1 \Rarr R \circ L$$

$$\epsilon : L \circ R \Rarr 1$$

Satisfying (for any object $G$):

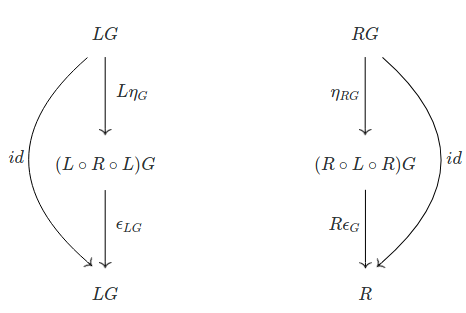
Defining $\epsilon$ is simple, as we saw before. Since $L \circ R$ is exactly the identity functor, we can simply take $id_G : (L \circ R) G \to G$ as the components of this natural transformation.

As far as $\eta$, this will likewise be the identity function, except for $\emptyset$. In this case, $\eta_{\emptyset} : \emptyset \to (R \circ L) \emptyset$ will be defined by the unique morphism $\emptyset \to 1$. The commuting diagram property of a natural transformation is clearly satisfied when it comes to $\emptyset$, because all morphisms out of it are unique.

Zig-Zag Properties

Are the special properties satisfied?

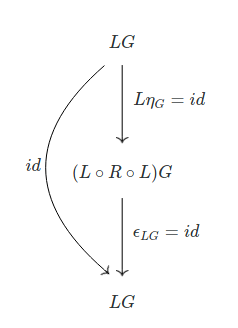
Left

Because $\eta$ is the identity, except when we’re working with the empty set, $L \eta$ will be the identity, except in that case. But, given $\varphi : \emptyset \to {e}$, $L \eta$ has to be a morphism ${e} \to {e}$ which can only be $id$.

And then $\epsilon$, by definition, is the identity.

So we have:

Right

Since $RG$ will never be the empty set, $\eta$ will be the identity. But then, we have that $\epsilon$ is the identity, so $R \epsilon$ must be the identity as well. Hence:

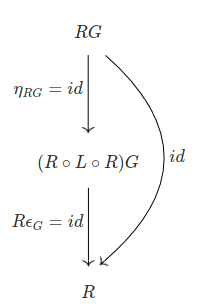
So, both properties hold, and we do indeed have an adjunction.

Conclusion

So, to answer the question we sort of asked before, are nonempty groups the same thing as potentially empty groups?

Yes and no.

Individually, these are the same thing.

As a whole, the existence of the empty group shifts things around a bit. In fact, it shifts things around enough so that the two categories are merely adjoint, and not equivalent nor isomorphic.

That being said, the two categories are much more connected than the minimum strictly necessary for an adjunction, and are still tightly related. The differences are also only related to the empty group. With minor adjustment, global statements about the structure of $\bold{Grp}$ can be accomodated to $\bold{Gr}\emptyset\bold{up}$ with perhaps an exception being made for the empty group.